 |
OEIS |
numbers having multiplicative digital root 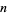 |
| 0 |
A034048 |
0, 10, 20, 25, 30, 40, 45, 50, 52, 54, 55, 56, 58, ... |
| 1 |
A002275 |
1, 11, 111, 1111, 11111, 111111, 1111111, 11111111, ... |
| 2 |
A034049 |
2, 12, 21, 26, 34, 37, 43, 62, 73, 112, 121, 126, ... |
| 3 |
A034050 |
3, 13, 31, 113, 131, 311, 1113, 1131, 1311, 3111, ... |
| 4 |
A034051 |
4, 14, 22, 27, 39, 41, 72, 89, 93, 98, 114, 122, ... |
| 5 |
A034052 |
5, 15, 35, 51, 53, 57, 75, 115, 135, 151, 153, 157, ... |
| 6 |
A034053 |
6, 16, 23, 28, 32, 44, 47, 48, 61, 68, 74, 82, 84, ... |
| 7 |
A034054 |
7, 17, 71, 117, 171, 711, 1117, 1171, 1711, 7111, ... |
| 8 |
A034055 |
8, 18, 24, 29, 36, 38, 42, 46, 49, 63, 64, 66, 67, ... |
| 9 |
A034056 |
9, 19, 33, 91, 119, 133, 191, 313, 331, 911, 1119, ... |


