


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-10-2020
Date: 16-1-2021
Date: 29-11-2020
|
Let 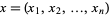 and
and 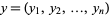 be nonincreasing sequences of real numbers. Then
be nonincreasing sequences of real numbers. Then  majorizes
majorizes 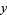 if, for each
if, for each 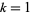 , 2, ...,
, 2, ..., 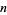 ,
,
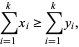 |
with equality if 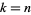 . Note that some caution is needed when consulting the literature, since the direction of the inequality is not consistent from reference to reference. An order-free characterization along the lines of Horn's theorem is also readily available.
. Note that some caution is needed when consulting the literature, since the direction of the inequality is not consistent from reference to reference. An order-free characterization along the lines of Horn's theorem is also readily available.
 majorizes
majorizes 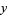 iff there exists a doubly stochastic matrix
iff there exists a doubly stochastic matrix 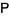 such that
such that 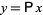 . Intuitively, if
. Intuitively, if  majorizes
majorizes 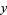 , then
, then 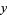 is more "mixed" than
is more "mixed" than  . Horn's theorem relates the eigenvalues of a Hermitian matrix
. Horn's theorem relates the eigenvalues of a Hermitian matrix 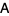 to its diagonal entries using majorization. Given two vectors
to its diagonal entries using majorization. Given two vectors 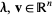 , then
, then 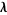 majorizes
majorizes 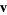 iff there exists a Hermitian matrix
iff there exists a Hermitian matrix 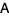 with eigenvalues
with eigenvalues 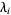 and diagonal entries
and diagonal entries 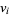 .
.
REFERENCES:
Bhatia, R. Matrix Analysis. New York: Springer-Verlag, 1997.
Horn, R. A. and Johnson, C. R. Matrix Analysis, Repr. with Corrections. Cambridge, England: Cambridge University Press, 1987.
Marshall, A. W. and Olkin, I. Inequalities: The Theory of Majorizations and Its Applications. New York: Academic Press, 1979.
Nielsen, M. A. "Conditions for a Class of Entanglement Transformations." Phys. Rev. Lett. 83, 436-439, 1999.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
|
|
|