المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Legendre Transform |
 736
 03:03 مساءً
date: 29-10-2020 |
Author : Jin, Y. and Dickinson, H. 
Book or Source : "Apéry Sequences and Legendre Transforms." J. Austral. Math. Soc. Ser. A 68, 
Page and Part : ...|
Read More
Date: 4-11-2019
886
Date: 9-6-2020
1029
Date: 20-8-2020
775
|
The Legendre transform of a sequence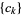 
is the sequence 
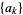with terms given by
 |
 |
 |
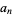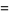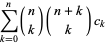(1) |
 |
 |
 |
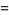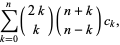(2) |
where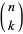 
is a binomial coefficient (Jin and Dickinson 2000, Zudilin 2004). The inverse Legendre transform is then given by
 |
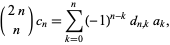(3) |
where
 |
 |
 |
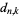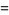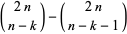(4) |
 |
 |
 |
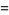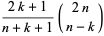(5) |
(Zudilin 2004).
Strehl (1994) and Schmidt (1995) showed that
 |
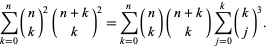(6) |
REFERENCES:
Jin, Y. and Dickinson, H. "Apéry Sequences and Legendre Transforms." J. Austral. Math. Soc. Ser. A 68, 349-356, 2000.
Schmidt, A. L. "Legendre Transforms and Apéry's Sequences." J. Austral. Math. Soc. Ser. A 58, 358-375, 1995.
Strehl, V. "Binomial Identities--Combinatorial and Algorithmic Aspects. Trends in Discrete Mathematics." Disc. Math. 136, 309-346, 1994.
Zudilin, W. "On a Combinatorial Problem of Asmus Schmidt." Elec. J. Combin. 11, R22, 1-8, 2004. https://www.combinatorics.org/Volume_11/Abstracts/v11i1r22.html.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
بالصور: ممثل المرجعية العليا الشيخ عبد المهدي الكربلائي يؤم جموع المؤمنين في صلاة عيد الفطر المبارك داخل الصحن الحسيني الشريف
|
|
|
