


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-10-2019
Date: 3-6-2019
Date: 18-6-2019
|
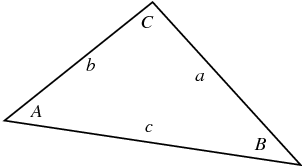
Let 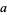 ,
, 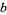 , and
, and 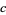 be the lengths of the legs of a triangle opposite angles
be the lengths of the legs of a triangle opposite angles 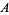 ,
, 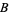 , and
, and 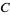 . Then the law of cosines states
. Then the law of cosines states
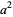 |
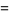 |
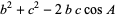 |
(1) |
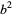 |
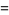 |
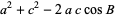 |
(2) |
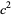 |
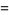 |
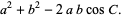 |
(3) |
Solving for the cosines yields the equivalent formulas
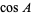 |
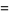 |
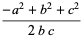 |
(4) |
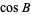 |
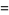 |
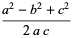 |
(5) |
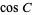 |
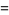 |
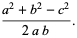 |
(6) |
This law can be derived in a number of ways. The definition of the dot product incorporates the law of cosines, so that the length of the vector from 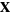 to
to 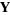 is given by
is given by
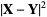 |
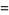 |
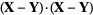 |
(7) |
 |
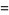 |
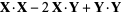 |
(8) |
 |
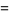 |
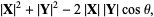 |
(9) |
where 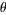 is the angle between
is the angle between 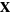 and
and 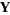 .
.
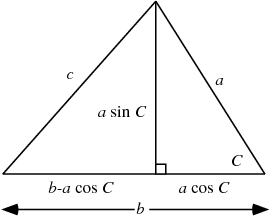
The formula can also be derived using a little geometry and simple algebra. From the above diagram,
 |
 |
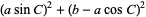 |
(10) |
 |
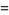 |
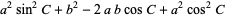 |
(11) |
 |
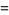 |
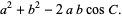 |
(12) |
The law of cosines for the sides of a spherical triangle states that
 |
 |
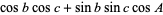 |
(13) |
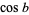 |
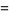 |
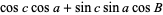 |
(14) |
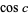 |
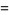 |
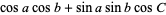 |
(15) |
(Beyer 1987). The law of cosines for the angles of a spherical triangle states that
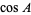 |
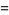 |
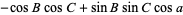 |
(16) |
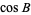 |
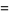 |
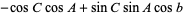 |
(17) |
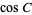 |
 |
 |
(18) |
(Beyer 1987).
For similar triangles, a generalized law of cosines is given by
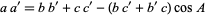 |
(19) |
(Lee 1997). Furthermore, consider an arbitrary tetrahedron 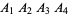 with triangles
with triangles 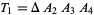 ,
, 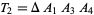 ,
, 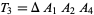 , and
, and 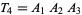 . Let the areas of these triangles be
. Let the areas of these triangles be  ,
,  ,
,  , and
, and 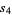 , respectively, and denote the dihedral angle with respect to
, respectively, and denote the dihedral angle with respect to 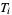 and
and 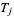 for
for 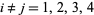 by
by 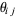 . Then
. Then
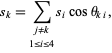 |
(20) |
which gives the law of cosines in a tetrahedron,
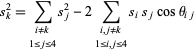 |
(21) |
(Lee 1997). A corollary gives the nice identity
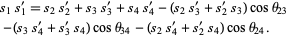 |
(22) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 79, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 148-149, 1987.
Lee, J. R. "The Law of Cosines in a Tetrahedron." J. Korea Soc. Math. Ed. Ser. B: Pure Appl. Math. 4, 1-6, 1997.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|