المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Whipple,s Identity |
 1931
 06:30 مساءً
date: 18-6-2019 |
Author : Graham, R. L.; Knuth, D. E.; and Patashnik, O. 
Book or Source : Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994. 
Page and Part : ...|
Read More
Date: 25-5-2019
1541
Date: 25-5-2019
2449
Date: 24-9-2019
1913
|
Whipple derived a great many identities for generalized hypergeometric functions, many of which are consequently known as Whipple's identities (transformations, etc.). Among Whipple's identities include
![_3F_2[a,1-a,c; e,1+2c-e;1]
=(2^(1-2c)piGamma(e)Gamma(1+2c-e))/(Gamma[1/2(a+e)]Gamma[1/2(a+1+2c-e)])1/(Gamma[1/2(1-a+e)]Gamma[1/2(2+2c-a-e)])](http://mathworld.wolfram.com/images/equations/WhipplesIdentity/NumberedEquation1.gif) |
(Bailey 1935, p. 15; Koepf 1998, p. 32), where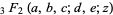 
is a generalized hypergeometric function and 
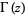is a gamma function, and
![_6F_5[a,1+1/2a,b,c,d,e; 1/2a,1+a-b,1-a+c,1+a-d,1+a-e;-1]
=(Gamma(1+a-d)Gamma(1+a-e))/(Gamma(1+a)Gamma(1+a-d-e))_3F_2[1+a-b-c,d,e; 1+a-b,1+a-c;1]](http://mathworld.wolfram.com/images/equations/WhipplesIdentity/NumberedEquation2.gif) |
(Bailey 1935, p. 28).
REFERENCES:
Bailey, W. N. "Whipple's Theorem on the Sum of a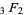 
." §3.4 in Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, p. 16, 1935.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.
Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, 1998.
Whipple, F. J. W. "Well-Poised Series and Other Generalized Hypergeometric Series." Proc. London Math. Soc. Ser. 2 25, 525-544, 1926.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
شعبة التوجيه الديني النسوي تنظم مسابقة ميدانية لزائرات مرقد أبي الفضل العباس (عليه السلام)
|
|
|
