Bernstein Polynomial

The polynomials defined by

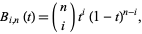(1)

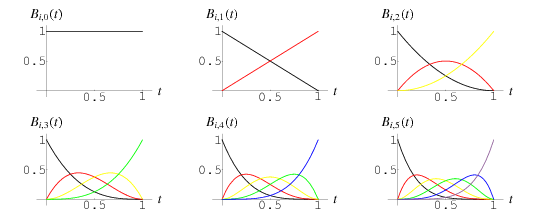
where 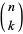 is a binomial coefficient. The Bernstein polynomials of degree  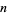form a basis for the power polynomials of degree 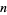. The first few polynomials are

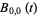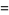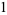			(2)
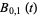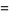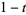			(3)
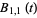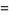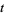			(4)
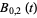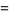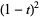			(5)
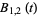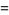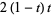			(6)
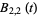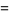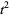			(7)
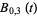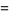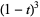			(8)
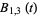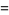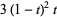			(9)
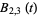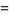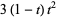			(10)
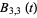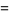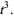			(11)

The Bernstein polynomials are implemented in the Wolfram Language as BernsteinBasis[n, i, t].

The Bernstein polynomials have a number of useful properties (Farin 1993). They satisfy symmetry

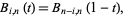(12)

positivity

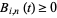(13)

for 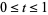, normalization

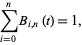(14)

and 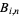 with 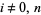 has a single unique local maximum of

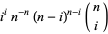(15)

occurring at .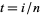

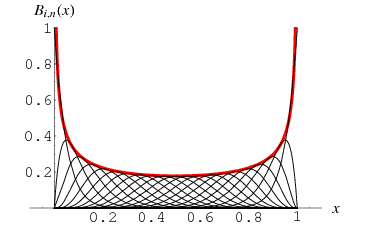
The envelope 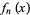 of the Bernstein polynomials  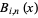for 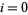, 1, ...,  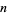(Mabry 2003) is given by

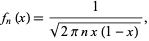(16)

illustrated above for .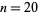

REFERENCES:

Bernstein, S. "Démonstration du théorème de Weierstrass fondée sur le calcul des probabilities." Comm. Soc. Math. Kharkov 13, 1-2, 1912.

Farin, G. Curves and Surfaces for Computer Aided Geometric Design. San Diego: Academic Press, 1993.

Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 2, 3rd ed. New York: Wiley, p. 222, 1971.

Kac, M. "Une remarque sur les polynomes de M. S. Bernstein." Studia Math. 7, 49-51, 1938.

Kac, M. "Reconnaissance de priorité relative à ma note, 'Une remarque sur les polynomes de M. S. Bernstein.' " Studia Math. 8, 170, 1939.

Lorentz, G. G. Bernstein Polynomials. Toronto: University of Toronto Press, 1953.

Mabry, R. "Problem 10990." Amer. Math. Monthly 110, 59, 2003.

Mathé, P. "Approximation of Hölder Continuous Functions by Bernstein Polynomials." Amer. Math. Monthly 106, 568-574, 1999.

Widder, D. V. The Laplace Transform. Princeton, NJ: Princeton University Press, p. 101, 1941.