


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-6-2019
Date: 29-4-2018
Date: 17-9-2019
|
The Rogers-Selberg identities are a set of three analytic q-series identities of Rogers-Ramanujan-type appearing as equation 33, 32, and 31 in Slater (1952),
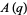 |
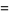 |
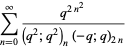 |
(1) |
 |
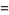 |
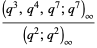 |
(2) |
 |
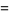 |
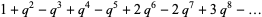 |
(3) |
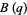 |
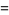 |
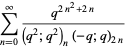 |
(4) |
 |
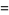 |
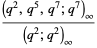 |
(5) |
 |
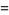 |
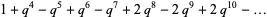 |
(6) |
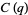 |
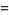 |
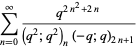 |
(7) |
 |
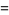 |
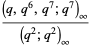 |
(8) |
 |
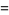 |
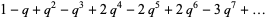 |
(9) |
(OEIS A104408, A104409, and A104410), where 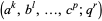 is extended q-series notation.
is extended q-series notation.
Andrews (1980) gave a technique for combinatorially interpreting the Rogers-Selberg identities.
The identities were discovered by Rogers (1894, 1917) and independently rediscovered by Selberg (1936) and Dyson (1943). They were subsequently generalized by Bailey (1947) before appearing in Slater's list of 130 identities of the Rogers-Ramanujan type (Slater 1952).
REFERENCES:
Andrews, G. E. "Gap-Frequency Partitions and the Rogers-Selberg Identities." Ars. Combin. 9, 201-210, 1980.
Bailey, W. N. "Some Identities in Combinatory Analysis." Proc. London Math. Soc. 49, 421-425, 1947.
Dyson, F. J. "Three Identities in Combinatory Analysis." J. London Math. Soc. 18, 35-39, 1943.
Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, pp. 36-37, 1990.
Hahn, H. "Septic Analogues of the Rogers-Ramanujan Functions." Acta Arith. 110, 381-399, 2003.
Mc Laughlin, J.; Sills, A. V.; and Zimmer, P. "Dynamic Survey DS15: Rogers-Ramanujan-Slater Type Identities." Electronic J. Combinatorics, DS15, 1-59, May 31, 2008. http://www.combinatorics.org/Surveys/ds15.pdf.
Milne, S. C. "Classical Partition Functions and the 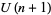 Rogers-Selberg Identity." Disc. Math. 99, 199-246, 1992.
Rogers-Selberg Identity." Disc. Math. 99, 199-246, 1992.
Rogers, L. J. "On the Expansion of Some Infinite Products. Part 2." Proc. London Math. Soc. 25, 318-343, 1894.
Rogers, L. J. "On Two Theorems of Combinatory Analysis and Some Allied Identities." Proc. London Math. Soc. 16, 315-336, 1917.
Selberg, A. "Über einige arithmetische Identitäten." Avh. Norske Vid.-Akad. Oslo I, No. 8, 1-23, 1936.
Slater, L. J. "Further Identities of the Rogers-Ramanujan Type." Proc. London Math. Soc. Ser. 2 54, 147-167, 1952.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|