المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Weber-Sonine Formula |
 1610
 02:37 مساءً
date: 30-3-2019 |
Author : Iyanaga, S. and Kawada, Y. 
Book or Source : Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press 
Page and Part : ...|
Read More
Date: 29-9-2018
2143
Date: 23-5-2019
1703
Date: 13-8-2019
3011
|
For ![R[mu+nu]>0](http://mathworld.wolfram.com/images/equations/Weber-SonineFormula/Inline1.gif)
, 
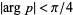, and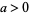 
,
![int_0^inftyJ_nu(at)e^(-p^2t^2)t^(mu-1)dt=(a/(2p))^nu(Gamma[1/2(nu+mu)])/(2p^muGamma(nu+1))_1F_1(1/2(nu+mu);nu+1;-(a^2)/(4p^2)),](http://mathworld.wolfram.com/images/equations/Weber-SonineFormula/NumberedEquation1.gif) |
where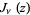 
is a Bessel function of the first kind, 
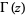is the gamma function, and 
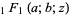is a confluent hypergeometric function of the first kind.
REFERENCES:
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1474, 1980.
Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, p. 393, 1966.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
