Subresultant

Subresultants can be viewed as a generalization of resultants, which are the product of the pairwise differences of the roots of polynomials. Subresultants are the most commonly used tool to compute the resultant or greatest common divisor of two polynomials with coefficients in an integral ring. Subresultants for a few simple pairs of polynomials include

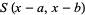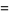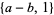			(1)
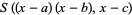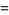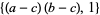			(2)
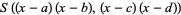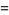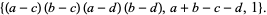			(3)

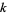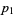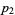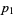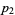The principal subresultants of two polynomials can be computed using the Wolfram Language function Subresultants[poly1, poly2, var]. The first  subresultants of two polynomials  and , both with leading coefficient one, are zero when  and  have 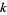 common roots.

REFERENCES:

Akritas, A. G. Elements of Computer Algebra with Applications. New York: Wiley, 1989.

Cohen, H. Ch. 3 in A Course in Computational Algebraic Number Theory. Berlin: Springer-Verlag, 1993.

D'Andrea, C.; Krick, T.; and Szanto, A. "Multivariate Subresultants in Roots." 28 Jul 2005. http://arxiv.org/abs/math.AG/0501281.

Ducos, L. "Optimizations of the Subresultant Algorithm." J. Pure Appl. Algebra 145, 149-163, 2000.

Geddes, K. O.; Czapor, S. R.; and Labahn, G. Algorithms for Computer Algebra. Amsterdam, Netherlands: Kluwer, 1992.

Hong, H. "Subresultants Under Composition." J. Symb. Comput. 23, 355-365, 1997.

Hong, H. "Subresultants in Roots." Submitted 1999. http://www4.ncsu.edu/~hong/papers/Hong99a.html.