


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-3-2017
Date: 17-1-2019
Date: 19-1-2019
|
The highest order power in a univariate polynomial is known as its order (or, more properly, its polynomial degree). For example, the polynomial
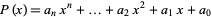 |
is of order 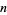 , denoted
, denoted 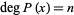 . The order of a polynomial is implemented in the Wolfram Language as Exponent[poly, x].
. The order of a polynomial is implemented in the Wolfram Language as Exponent[poly, x].
It is preferable to use the word "degree" for the highest exponent in a polynomial, since a completely different meaning is given to the word "order" in polynomials taken modulo some integer (where this meaning is the one used in themultiplicative order of a modulus). In particular, the order of a polynomial 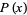 with
with 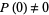 is the smallest integer
is the smallest integer 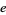 for which
for which 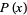 divides
divides 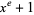 (Lidl and Niederreiter 1994). For example, in the finite field GF(2), the order of
(Lidl and Niederreiter 1994). For example, in the finite field GF(2), the order of 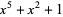 is 31, since
is 31, since
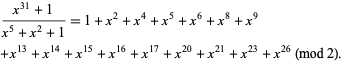 |
This concept is closely related to that of the multiplicative order.
If 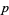 is an irreducible polynomial of degree
is an irreducible polynomial of degree 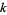 , then its order has to divide the order of the multiplicative group in the corresponding field extension, i.e.,
, then its order has to divide the order of the multiplicative group in the corresponding field extension, i.e., 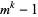 for modulus
for modulus 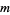 .
.
REFERENCES:
Lidl, R. and Niederreiter, H. Introduction to Finite Fields and their Applications, 2nd ed. New York: Cambridge University Press, 1994.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|