


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-1-2019
Date: 17-2-2019
Date: 19-1-2019
|
The 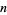 th coefficient in the power series of a univalent function should be no greater than
th coefficient in the power series of a univalent function should be no greater than 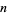 . In other words, if
. In other words, if
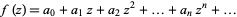 |
is a conformal mapping of a unit disk on any domain and 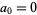 and
and 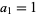 , then
, then 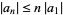 . In more technical terms, "geometric extremality implies metric extremality." An alternate formulation is that
. In more technical terms, "geometric extremality implies metric extremality." An alternate formulation is that 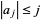 for any schlicht function
for any schlicht function 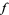 (Krantz 1999, p. 150).
(Krantz 1999, p. 150).
The conjecture had been proven for the first six terms (the cases 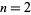 , 3, and 4 were done by Bieberbach, Lowner, and Garabedian and Schiffer, respectively), was known to be false for only a finite number of indices (Hayman 1954), and true for a convex or symmetric domain (Le Lionnais 1983). The general case was proved by Louis de Branges (1985). de Branges proved the Milin conjecture, which established the Robertson conjecture, which in turn established the Bieberbach conjecture (Stewart 1996).
, 3, and 4 were done by Bieberbach, Lowner, and Garabedian and Schiffer, respectively), was known to be false for only a finite number of indices (Hayman 1954), and true for a convex or symmetric domain (Le Lionnais 1983). The general case was proved by Louis de Branges (1985). de Branges proved the Milin conjecture, which established the Robertson conjecture, which in turn established the Bieberbach conjecture (Stewart 1996).
| author | result |
| Bieberbach (1916) | 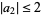 |
| Löwner (1923) | 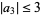 |
| Garabedian and Schiffer (1955) | 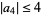 |
| Pederson (1968), Ozawa (1969) | 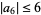 |
| Pederson and Schiffer (1972) | 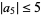 |
| de Branges (1985) | 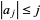 for all for all 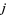 |
The sum
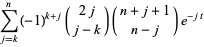 |
was an essential tool in de Branges' proof (Koepf 1998, p. 29).
REFERENCES:
Bieberbach, L. "Über die Koeffizienten derjenigen Potenzreihen, welche eine schlichte Abbildung des Einheitskreises vermitteln." Sitzungsber. Preuss. Akad. Wiss., pp. 940-955, 1916.
Charzynski, Z. and Schiffer, M. "A New Proof of the Bieberbach Conjecture for the Fourth Coefficient." Arch. Rational Mech. Anal.5, 187-193, 1960.
de Branges, L. "A Proof of the Bieberbach Conjecture." Acta Math. 154, 137-152, 1985.
Duren, P.; Drasin, D.; Bernstein, A.; and Marden, A. The Bieberbach Conjecture: Proceedings of the Symposium on the Occasion of the Proof. Providence, RI: Amer. Math. Soc., 1986.
Garabedian, P. R. "Inequalities for the Fifth Coefficient." Comm. Pure Appl. Math. 19, 199-214, 1966.
Garabedian, P. R.; Ross, G. G.; and Schiffer, M. "On the Bieberbach Conjecture for Even n." J. Math. Mech. 14, 975-989, 1965.
Garabedian, R. and Schiffer, M. "A Proof of the Bieberbach Conjecture for the Fourth Coefficient." J. Rational Mech. Anal. 4, 427-465, 1955.
Gong, S. The Bieberbach Conjecture. Providence, RI: Amer. Math. Soc., 1999.
Hayman, W. K. Multivalent Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1994.
Hayman, W. K. and Stewart, F. M. "Real Inequalities with Applications to Function Theory." Proc. Cambridge Phil. Soc. 50, 250-260, 1954.
Kazarinoff, N. D. "Special Functions and the Bieberbach Conjecture." Amer. Math. Monthly 95, 689-696, 1988.
Koepf, W. "Hypergeometric Identities." Ch. 2 in Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, p. 29, 1998.
Korevaar, J. "Ludwig Bieberbach's Conjecture and its Proof." Amer. Math. Monthly 93, 505-513, 1986.
Krantz, S. G. "The Bieberbach Conjecture." §12.1.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 149-150, 1999.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 53, 1983.
Löwner, K. "Untersuchungen über schlichte konforme Abbildungen des Einheitskreises. I." Math. Ann. 89, 103-121, 1923.
Ozawa, M. "On the Bieberbach Conjecture for the Sixth Coefficient." Kodai Math. Sem. Rep. 21, 97-128, 1969.
Pederson, R. N. "On Unitary Properties of Grunsky's Matrix." Arch. Rational Mech. Anal. 29, 370-377, 1968.
Pederson, R. N. "A Proof of the Bieberbach Conjecture for the Sixth Coefficient." Arch. Rational Mech. Anal. 31, 331-351, 1968/1969.
Pederson, R. and Schiffer, M. "A Proof of the Bieberbach Conjecture for the Fifth Coefficient." Arch. Rational Mech. Anal. 45, 161-193, 1972.
Stewart, I. "The Bieberbach Conjecture." In From Here to Infinity: A Guide to Today's Mathematics. Oxford, England: Oxford University Press, pp. 164-166, 1996.
Weinstein, L. "The Bieberbach Conjecture." Internat. Math. Res. Not. 5, 61-64, 1991.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|