المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Argument Principle |
 507
 02:19 مساءً
date: 17-11-2018 |
Author : Duren, P.; Hengartner, W.; and Laugessen, R. S 
Book or Source : "The Argument Principle for Harmonic Functions." Amer. Math. Monthly 103 
Page and Part : ...|
Read More
Date: 17-11-2018
351
Date: 16-12-2018
532
Date: 18-10-2018
425
|
If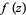 
is meromorphic in a region 
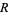enclosed by a contour 
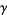, let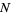 
be the number of complex roots of 
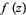in 
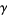, and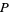 
be the number of poles in 
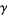, with each zero and pole counted as many times as its multiplicity and order, respectively. Then
 |
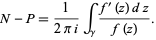Defining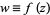 
and 
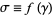gives
 |
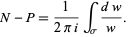REFERENCES:
Duren, P.; Hengartner, W.; and Laugessen, R. S. "The Argument Principle for Harmonic Functions." Amer. Math. Monthly 103, 411-415, 1996.
Knopp, K. Theory of Functions, Parts I and II. New York: Dover, pp. 132-134, 1996.
Krantz, S. G. "The Argument Principle." Ch. 5 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 69-78, 1999.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
