
Complex Differentiable
 المؤلف:
Shilov, G. E
المؤلف:
Shilov, G. E
 المصدر:
Elementary Real and Complex Analysis. New York: Dover
المصدر:
Elementary Real and Complex Analysis. New York: Dover
 الجزء والصفحة:
p. 379
الجزء والصفحة:
p. 379
 18-10-2018
18-10-2018
 931
931
Complex Differentiable
Let 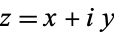 and
and 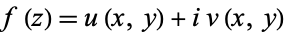 on some region
on some region  containing the point
containing the point 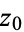 . If
. If 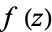 satisfies the Cauchy-Riemann equations and has continuous first partial derivatives in the neighborhood of
satisfies the Cauchy-Riemann equations and has continuous first partial derivatives in the neighborhood of 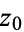 , then
, then 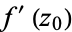 exists and is given by
exists and is given by
and the function is said to be complex differentiable (or, equivalently, analytic or holomorphic).
A function 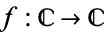 can be thought of as a map from the plane to the plane,
can be thought of as a map from the plane to the plane, 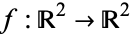 . Then
. Then 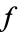 is complex differentiable iff its Jacobian is of the form
is complex differentiable iff its Jacobian is of the form
at every point. That is, its derivative is given by the multiplication of a complex number 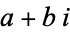 . For instance, the function
. For instance, the function 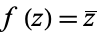 , where
, where 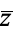 is the complex conjugate, is not complex differentiable.
is the complex conjugate, is not complex differentiable.
REFERENCES:
Shilov, G. E. Elementary Real and Complex Analysis. New York: Dover, p. 379, 1996.
 الاكثر قراءة في التحليل العقدي
الاكثر قراءة في التحليل العقدي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


