Lane-Emden Differential Equation

A second-order ordinary differential equation arising in the study of stellar interiors, also called the polytropic differential equations. It is given by

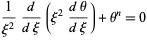(1)

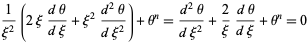(2)

(Zwillinger 1997, pp. 124 and 126). It has the boundary conditions

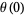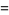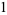			(3)
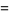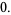			(4)

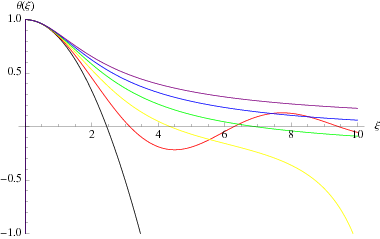
Solutions 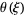 for 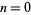, 1, 2, 3, and 4 are shown above. The cases 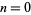, 1, and 5 can be solved analytically (Chandrasekhar 1967, p. 91); the others must be obtained numerically.

For 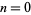 (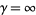), the Lane-Emden differential equation is

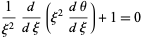(5)

(Chandrasekhar 1967, pp. 91-92). Directly solving gives

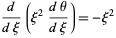(6)

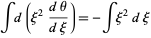(7)

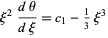(8)

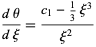(9)

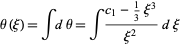(10)

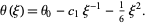(11)

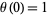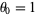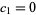The boundary condition  then gives  and , so

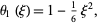(12)

and 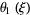 is parabolic.

For 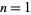 (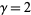), the differential equation becomes

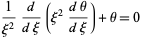(13)

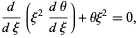(14)

which is the spherical Bessel differential equation

(15)

with 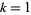 and 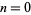, so the solution is

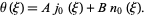(16)

Applying the boundary condition 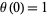 gives

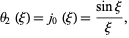(17)

where 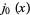 is a spherical Bessel function of the first kind (Chandrasekhar 1967, p. 92).

For 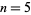, make Emden's transformation

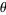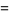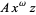			(18)
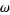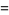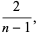			(19)

which reduces the Lane-Emden equation to

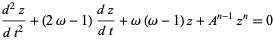(20)

(Chandrasekhar 1967, p. 90). After further manipulation (not reproduced here), the equation becomes

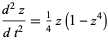(21)

and then, finally,

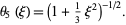(22)

REFERENCES:

Chandrasekhar, S. An Introduction to the Study of Stellar Structure. New York: Dover, pp. 84-182, 1967.

Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 908, 1980.

Seshadri, R. and Na, T. Y. Group Invariance in Engineering Boundary Value Problems. New York: Springer-Verlag, p. 193, 1985.

Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, pp. 124 and 126, 1997.