


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-12-2018
Date: 5-7-2018
Date: 13-6-2018
|
Given a system of ordinary differential equations of the form
![d/(dt)[x; y; v_x; v_y]=-[0 0 -1 0; 0 0 0 -1; Phi_(xx)(t) Phi_(yx)(t) 0 0; Phi_(xy)(t) Phi_(yy)(t) 0 0][x; y; v_x; v_y]](http://mathworld.wolfram.com/images/equations/FloquetAnalysis/NumberedEquation1.gif) |
(1) |
that are periodic in 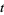 , the solution can be written as a linear combination of functions of the form
, the solution can be written as a linear combination of functions of the form
![[x(t); y(t); v_x(t); v_y(t)]=[x_0; y_0; v_(x0); v_(y0)]e^(mut)P_mu(t),](http://mathworld.wolfram.com/images/equations/FloquetAnalysis/NumberedEquation2.gif) |
(2) |
where 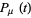 is a function periodic with the same period
is a function periodic with the same period 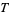 as the equations themselves. Given an ordinary differential equation of the form
as the equations themselves. Given an ordinary differential equation of the form
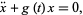 |
(3) |
where 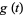 is periodic with period
is periodic with period 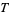 , the ODE has a pair of independent solutions given by the real and imaginary parts of
, the ODE has a pair of independent solutions given by the real and imaginary parts of
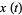 |
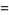 |
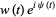 |
(4) |
 |
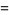 |
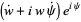 |
(5) |
 |
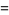 |
![[w^..+iw^.psi^.+i(w^.psi^.+wpsi^..+iwpsi^.^2)]e^(ipsi)](http://mathworld.wolfram.com/images/equations/FloquetAnalysis/Inline14.gif) |
(6) |
 |
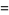 |
![[(w^..-wpsi^.^2)+i(2w^.psi^.+wpsi^..)]e^(ipsi).](http://mathworld.wolfram.com/images/equations/FloquetAnalysis/Inline17.gif) |
(7) |
Plugging these into (◇) gives
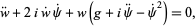 |
(8) |
so the real and imaginary parts are
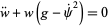 |
(9) |
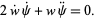 |
(10) |
From (◇),
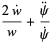 |
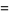 |
![2d/(dt)(lnw)+d/(dt)[ln(psi^.)]](http://mathworld.wolfram.com/images/equations/FloquetAnalysis/Inline20.gif) |
(11) |
 |
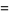 |
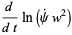 |
(12) |
 |
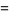 |
 |
(13) |
Integrating gives
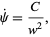 |
(14) |
where 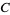 is a constant which must equal 1, so
is a constant which must equal 1, so 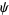 is given by
is given by
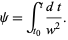 |
(15) |
The real solution is then
![x(t)=w(t)cos[psi(t)],](http://mathworld.wolfram.com/images/equations/FloquetAnalysis/NumberedEquation9.gif) |
(16) |
so
 |
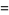 |
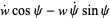 |
(17) |
 |
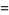 |
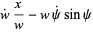 |
(18) |
 |
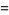 |
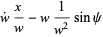 |
(19) |
 |
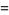 |
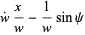 |
(20) |
and
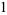 |
 |
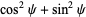 |
(21) |
 |
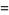 |
![x^2w^(-2)+[w(w^.x/w-x^.)]^2](http://mathworld.wolfram.com/images/equations/FloquetAnalysis/Inline46.gif) |
(22) |
 |
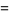 |
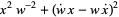 |
(23) |
 |
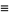 |
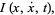 |
(24) |
which is an integral of motion. Therefore, although 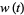 is not explicitly known, an integral
is not explicitly known, an integral 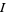 always exists. Plugging (◇) into (◇) gives
always exists. Plugging (◇) into (◇) gives
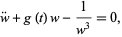 |
(25) |
which, however, is not any easier to solve than (◇).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 727, 1972.
Binney, J. and Tremaine, S. Galactic Dynamics. Princeton, NJ: Princeton University Press, p. 175, 1987.
Lichtenberg, A. and Lieberman, M. Regular and Stochastic Motion. New York: Springer-Verlag, p. 32, 1983.
Margenau, H. and Murphy, G. M. The Mathematics of Physics and Chemistry, 2 vols. Princeton, NJ: Van Nostrand, 1956-64.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 556-557, 1953.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|