


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-6-2018
Date: 11-6-2018
Date: 5-7-2018
|
 |
(1) |
or
 |
(2) |
The solutions are Jacobi polynomials 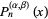 or, in terms of hypergeometric functions, as
or, in terms of hypergeometric functions, as
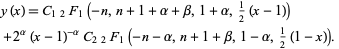 |
(3) |
The equation (2) can be transformed to
![(d^2u)/(dx^2)+[1/4(1-alpha^2)/((1-x)^2)+1/4(1-beta^2)/((1+x)^2)+(n(n+alpha+beta+1)+1/2(alpha+1)(beta+1))/(1-x^2)]u=0,](http://mathworld.wolfram.com/images/equations/JacobiDifferentialEquation/NumberedEquation4.gif) |
(4) |
where
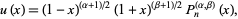 |
(5) |
and
![(d^2u)/(dtheta^2)+[(1/4-alpha^2)/(4sin^2(1/2theta))+(1/4-beta^2)/(4cos^2(1/2theta))+(n+(alpha+beta+1)/2)^2]u=0,](http://mathworld.wolfram.com/images/equations/JacobiDifferentialEquation/NumberedEquation6.gif) |
(6) |
where
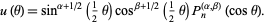 |
(7) |
Zwillinger (1997, p. 123) gives a related differential equation he terms Jacobi's equation
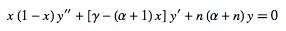 |
(8) |
(Iyanaga and Kawada 1980, p. 1480), which has solution
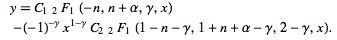 |
(9) |
Zwillinger (1997, p. 120; duplicated twice) also gives another types of ordinary differential equation called a Jacobi equation,
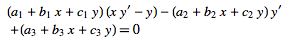 |
(10) |
(Ince 1956, p. 22).
In the calculus of variations, the partial differential equation
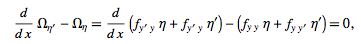 |
(11) |
where
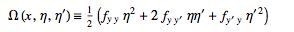 |
(12) |
is called the Jacobi differential equation.
REFERENCES:
Bliss, G. A. Calculus of Variations. Chicago, IL: Open Court, pp. 162-163, 1925.
Ince, E. L. Ordinary Differential Equations. New York: Dover, p. 22, 1956.
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1480, 1980.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 120, 1997.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|