
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-8-2018
Date: 11-6-2018
|
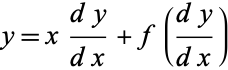 |
(1) |
or
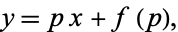 |
(2) |
where 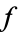 is a function of one variable and
is a function of one variable and 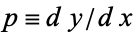 . The general solution is
. The general solution is
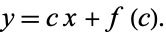 |
(3) |
The singular solution envelopes are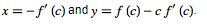 .
.
A partial differential equation known as Clairaut's equation is given by
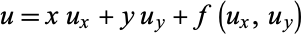 |
(4) |
(Iyanaga and Kawada 1980, p. 1446; Zwillinger 1997, p. 132).
REFERENCES:
Boyer, C. B. A History of Mathematics. New York: Wiley, p. 494, 1968.
Ford, L. R. Differential Equations. New York: McGraw-Hill, p. 16, 1955.
Ince, E. L. Ordinary Differential Equations. New York: Dover, pp. 39-40, 1956.
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1446, 1980.
Zwillinger, D. "Clairaut's Equation." §II.A.38 in Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, pp. 120 and 158-160, 1997.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة لجامعة سومر للمشاركة في حفل التخرج المركزي الخامس
|
|
|