Vectors and Their Components

The graphical method requires the use of a ruler and protractor for measuring the lengths of vectors and their angles. Thus there is always the problem of inaccuracy in making these measurements. It's better to use analytical methods which rely on pure calculation. To learn this we must learn about components. To do this we need trigonometry.

1. Review of Trigonometry

Lines are made by connecting two points. Triangles are made by connecting three points. Of all the vast number of different possible triangles, the subject of trigonometry has to do with only a certain, special type of triangle and that is a right-angled triangle, i.e. a triangle where one of the angles is 90^o. Let's draw one:

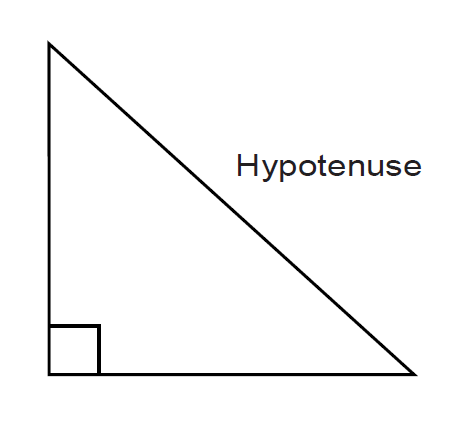
FIGURE 1.1 Right-angled triangle.

The side opposite the right angle is always called the Hypotenuse. Consider one of the other angles, say θ.

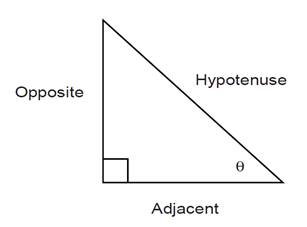
FIGURE 1.2 Right-angled triangle showing sides Opposite and Adjacent to the angle θ.

The side adjacent to θ is called Adjacent and the side opposite θ is called Opposite. Now consider the other angle α. The Opposite and Adjacent sides are switched because the angle is different.

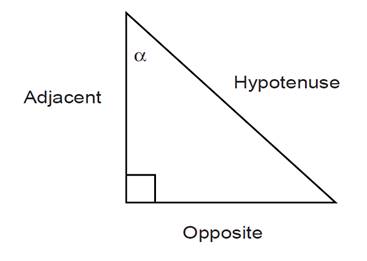
FIGURE 1.3 Right-angled triangle showing sides Opposite and Adjacent to the angle α.

Let's label Hypotenuse as H, Opposite as O and Adjacent as A. Pythagoras' theorem states

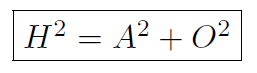
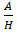This is true no matter how the Opposite and Adjacent sides are labelled, i.e. if Opposite and Adjacent are interchanged, it doesn't matter for Pythagoras' theorem. Often we are interested in dividing one side by another. Some possible these special ratios are given special names.  is called Sine.  is called Cosine.  is called Tangent. Remember them by writing SOH, CAH, TOA.

Example Using the previous triangle for the river problem, write down Sine θ, Cosine θ, Tangent θ Sine α, Cosine α, Tangent α

Solution

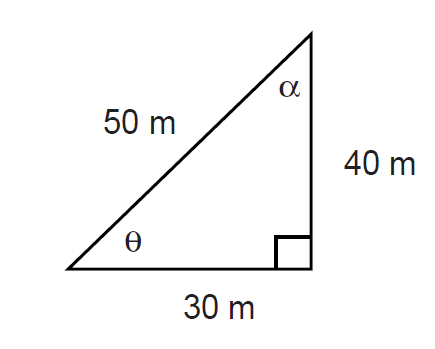
FIGURE 1.4 Triangle for river problem.

Now whenever the Sine of an angle is 0.8 the angle is always 53.1^o. Thus θ = 53:1^o. Again whenever Tangent of an angle is 0.75 the angle is always 36.9^o. So if we have calculated any of the ratios, Sine, Cosine or Tangent then we always know what the corresponding angle is.

2. Components of Vectors

An arbitrary vector has both x and y components. These are like shadows on the x and y areas, as shown in Figure 1.5.

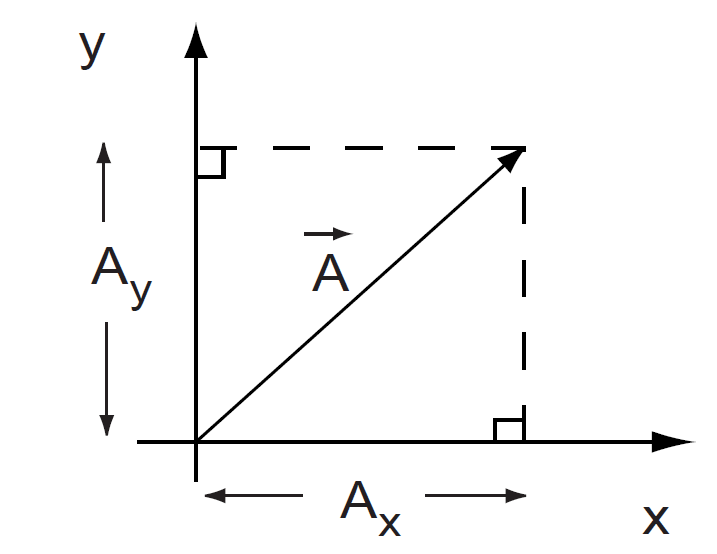
FIGURE 1.5 Components, A_x and A_y, of vector 

The components are denoted A_x and A_y and are obtained by dropping a perpendicular line from the vector to the x and y axes. That's why we consider trigonometry and right-angled triangles!

A physical understanding of components can be obtained. Pull a cart with a rope at some angle to the ground, as shown in Fig. 1.7. The cart will move with a certain acceleration, determined not by the force , but by the component F_x in the x direction. If you change the angle, the acceleration of the cart will change.

FIGURE 1.6 Pulling a cart with a force .

Let's re-draw Figure 1.6, writing instead of  as follows:

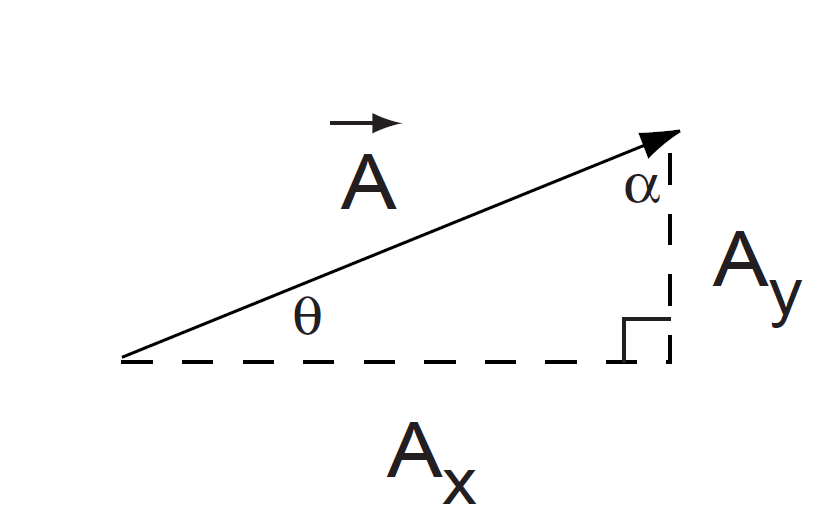
FIGURE 1.7 Components and angles for Fig. 1.6.

Let's denote the magnitude or length of 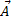simply as A. Thus Pythagoras' theorem gives

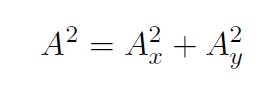
and also

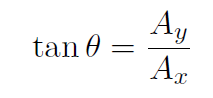
and

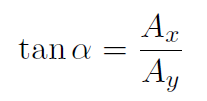
 (Also sin θ = 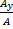, cos θ = 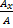, sin α = 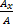, cos α = ).

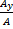Thus if we have the components, A_x and A_y we can always get the magnitude and direction of the vector, namely A and θ (or α). Similarly if we start with A and θ (or α) we can always find Ax and A_y.