


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-4-2022
Date: 7-4-2022
Date: 1-5-2022
|
We are going to define for edges, concepts equivalent to the one mentioned above. The edge connectivity 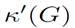 of a graph G, with more than one vertex, is the smallest number of edges by which removal disconnects the graph. In particular, it is 0 if the graph is disconnected. The edge connectivity is considered equal to 0 if the graph has only one vertex.
of a graph G, with more than one vertex, is the smallest number of edges by which removal disconnects the graph. In particular, it is 0 if the graph is disconnected. The edge connectivity is considered equal to 0 if the graph has only one vertex.
We can formalize the definition in this way. If the graph G has at least two vertices, it has a set of edges B, possibly empty, such that G − B is disconnected, and we put in that case:
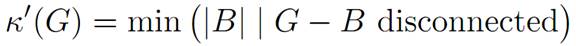
The set of edges B is what we call an (edge) cut of G. If G has only one vertex, we put:
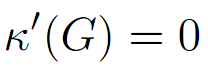
There is an inequality relation between connectivity and edge connectivity, given in the following proposition.
Proposition 1.1.
For any simple graph G, we have:
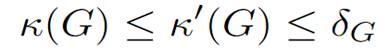
The second inequality is easy, the first can be shown directly but also results easily from Menger’s theorem (see later). These inequalities may be strict (find an example).
__________________________________________________________________________________
Graph Theory and Applications ,Jean-Claude Fournier, WILEY, page(63-64)



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|