RATE   EQUATIONS   AND   CRITERIA   FOR   LASING

         The general criteria for a net photon gain to occur (i.e., a laser gain) is that the rate of stimulated emission must exceed that of spontaneous emission plus that of all the losses. We begin by determining, mathematically, the parameters involved. The rate of absorption of photons depends on the number of atoms in the lower state (i.e., the number of atoms available to absorb photons) as well as the energy density of incident photons. The second parameter should be obvious: More photons to absorb leads to a higher rate of absorption. Mathematically, the rate of absorption may be stated as

r_absorption = B₁₂N₁ρ         (1.1)

where B₁₂ is a proportionality constant called Einstein’s coefficient, N₁ the number of atoms at the lower-energy state, and ρ the energy density. The energy density in this case is specific: It represents the number of photons that have the exact energy for the transition between energy levels E₁ and E₂. Similarly, the rate of stimulated emission depends on the number of atoms at the upper state and can be written as

r_stimulated = B₂₁N₂ρ     (1.2)

where B₂₁ is Einstein’s coefficient, N₂ the number of atoms at the upper energy state, and ρ the energy density.

        Finally, we must calculate the rate of spontaneous emission. This rate does not depend on incident energy density atoms emit photons spontaneously regardless of external conditions but solely on the number of atoms at the upper energy state available to emit a photon:

r_spontaneous =A₂₁N₂       (1.3)

where A₂₁ is Einstein’s coefficient for spontaneous emission and N₂ is the number of atoms at the upper energy state. It might be noted that the A coefficient for absorption is related to the spontaneous lifetime as

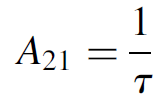 (1.4)

where τ is the spontaneous radiative lifetime of the upper state. Simply put, equation (1.3) states that the rate of spontaneous emission is equal to the number of atoms available in the upper state divided by the spontaneous lifetime (in seconds). It is calculated in units of s^-1 (the rates are in terms of number of atoms per second).

Example 1.1 The Role of Level Lifetimes The effect of level lifetimes on operation of a laser can be illustrated in a TEA (transverse electrical discharge at atmospheric pressure) nitrogen laser. Nitrogen has an exceptionally short upper lasing level lifetime of about 1.5 ns (at atmospheric pressure). Assume that nitrogen gas is placed in a long tube (like most other gas lasers) as in Figure 1.1 and is quickly pumped with energy to cause a population inversion. Assume now that a single photon is emitted spontaneously at the end of the tube (labeled A in the figure) and travels down the length of the tube being amplified along the way to produce an intense laser pulse. After 1.5 ns the laser pulse has traveled 0.45 m down the tube to the point labeled B. At this point, remaining excited nitrogen molecules in the tube (in front of the optical laser pulse now racing down the tube between points labeled B and C in Figure 1.1) have reached their spontaneous radiative lifetime and begin to emit light spontaneously, dropping to the lower level of the transition. Molecules in this state are strongly absorbing and absorb photons readily in the pulse traveling down the tube: The laser absorbs its own pulse and has no output.

           This situation seems to indicate that the tube cannot exceed 0.45 m in length; in reality, nitrogen lasers are not usually constructed using a longitudinal arrangement but rather a transverse arrangement in which the electrodes are parallel to the discharge tube. An electrical pulse is launched down the tube preceding the laser pulse, ensuring that the nitrogen gas is excited just before the laser pulse arrives to be amplified. This scheme ensures that the excited molecules do not stay in that state long enough to radiate radiation spontaneously before they get a chance to amplify the pulse traveling down the tube.

       As an aside, consider that in the nitrogen molecule the lower level has a much longer lifetime than the upper level. In such a system, continuous wave (CW) laser action may not be possible, as is the case here. The mechanism of the nitrogen laser itself must ensure that the upper level is quickly pumped with energy (in much less than 1.5 ns) to generate a population inversion. In the case of a transverse-

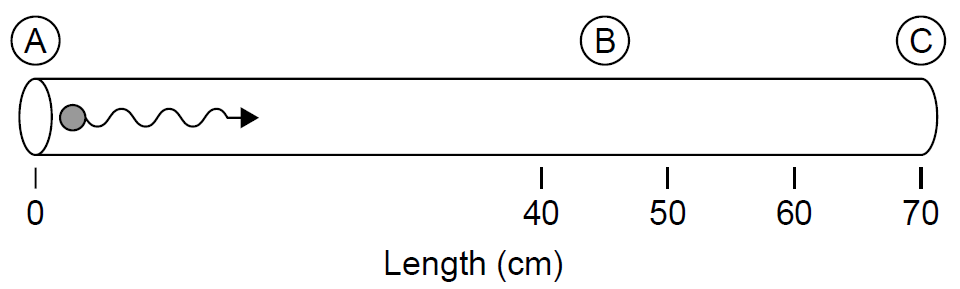
Figure 1.1. Hypothetical nitrogen laser tube.

discharge laser such as a nitrogen laser, a discharge of 10,000 A or more occurs.

      Let us proceed by equating rates at thermal equilibrium. It is assumed, then, that there is no external energy input to the system. We equate the rate of upward transitions (absorption) with the total rate of downward transitions (spontaneous and stimulated emission):

   r_absorption = r_stimulated +‏ r_spontaneous

or

B₁₂N₁ρ = B₂₁N₂ρ ‏+ A₂₁N₂   (1.5)

We now use Planck’s blackbody radiation law as well as Boltzmann’s law to solve for the energy density ρ. That Planck’s radiation law for cavity radiation is

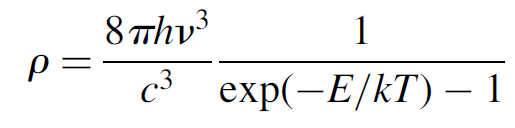 (1.6)

We can substitute into (1.6) as follows using Boltzmann’s law to ratio the populations of atoms at each energy level: exp(-E/kT) = N₂/N₁ provided that E is the energy difference between levels E₂ and E₁, so that

 (1.7)

Rearranging to solve for energy density in the original rate equation (1.3), we now find that

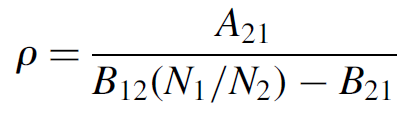 (1.8)

The two Einstein B coefficients represent the probability of an atom making the upward transition E₁ and E₂ and the downward transition E₂ to E₁, respectively. These are equal, so we shall now use the generalized term B:

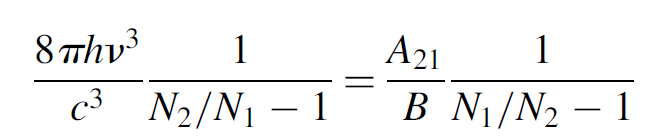
yielding

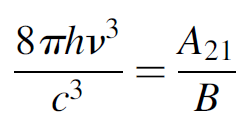 (1.9)

Now that we have a solution for the Einstein rate equations, we can draw some mathematical conclusions.

      Consider the ratio of stimulated to spontaneous emission. As we have already discussed, the rate of stimulated emission must exceed that of spontaneous emission for laser action to occur (in order to have amplification occur):

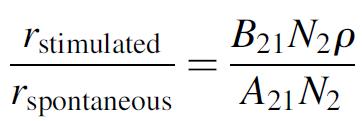 (1.10)

Substituting for the Einstein coefficients, this ratio simplifies to

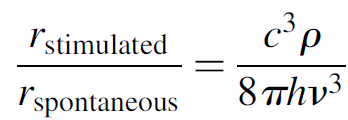 (1.11)

It is further possible to solve the ratio outright by substituting for ρ using Planck’s law from equation (1.6). We know the energy levels involved, hence we know the frequency of emitted photons v.

      An important conclusion at this stage is that for this ratio to be large (i.e., stimulated emission rate exceeds spontaneous rate), the energy density of incident photons must be high. This is the actual flux of photons within the laser cavity itself. Unless the gain of the medium is extremely high in order to create a huge flux of photons as they pass down the tube, cavity mirrors will be required to contain photons within the cavity to create further amplification. Indeed, the vast majority of lasers require cavity mirrors for oscillation. Furthermore, these mirrors are usually very efficient (> 95%) reflectors. We also note that the ratio of these rates also depends on the inverse of the frequency, cubed. In other words, higher frequencies (shorter wavelengths) have lower ratios and require higher energy densities to operate. As an aside, consider that the first laser operated at microwave frequencies, where much lower energy densities are required to favor this ratio over optical frequencies.

      The last concern is the rate of absorption of photons. We must ensure that photons emitted are not absorbed within the medium itself. If the medium absorbs more photons than were emitted by stimulated emission, the laser cannot work. This ratio is calculated directly from equations (1.1) and (1.2) as

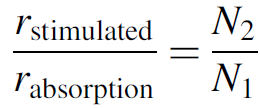 (1.12)

But in our case we have a population inversion where N₂ > N₁, so the rate of stimulated emission will indeed exceed the absorption rate. This relation proves the necessity of population inversion for laser action (for which we have given only a qualitative argument so far). This is a simple introduction to the rate equations, which can become considerably more complex, especially when multiple levels other than just the two lasing levels are involved (which they are in a real laser).

Example 1.2 Fiber Amplifiers In telecommunications systems employing laser emitters and long runs of fiber-optic cables, fiber amplifiers are used to boost weak signals optically. A practical amplifier consists of a long (10- to 20-m) section of glass fiber doped with erbium ions (Er³⁺‏). A pump laser at 980 nm is coupled to the amplifier fiber via a coupler. This pump radiation is absorbed by the erbium atoms in the fiber, exciting them to an upper level which rapidly decays to a level 0.80 eV above ground state. This level, which has a relatively long spontaneous radiative lifetime (τ_sp, about 10 ms long) can amplify incoming signals via stimulated emission, producing a net optical gain at 1549 nm. A diagram of this amplifier is depicted in Figure 1.2.

      Atoms in the fiber are excited continually by the pump laser. Weak incoming photons from the input fiber stimulate the emission of more photons in the fiber amplifier, producing a cascade of identical photons, which in effect amplifies the original signal. The fiber amplifier is just that: an amplifier. Unlike a laser, it lacks the ability to oscillate and hence requires a “seed” signal to amplify (i.e., the input signal).

        Like any other system with excited atoms, spontaneous emission can occur from the upper energy level of the atoms in the fiber. Spontaneous emission in the band of wavelengths at which the amplifier operates (centered around 1549 nm, the wavelength of the laser used for fiber communications) will be amplified producing amplified stimulated emission (ASE), which is seen as noise in the output of the device. When no input signal is present, the output of the amplifier consists of a good deal of ASE, as evident in Figure 1.3(b), which shows the output as analyzed by an optical spectrum analyzer (OSA), showing the amplitude at each wavelength. In a communications system, ASE is noise.

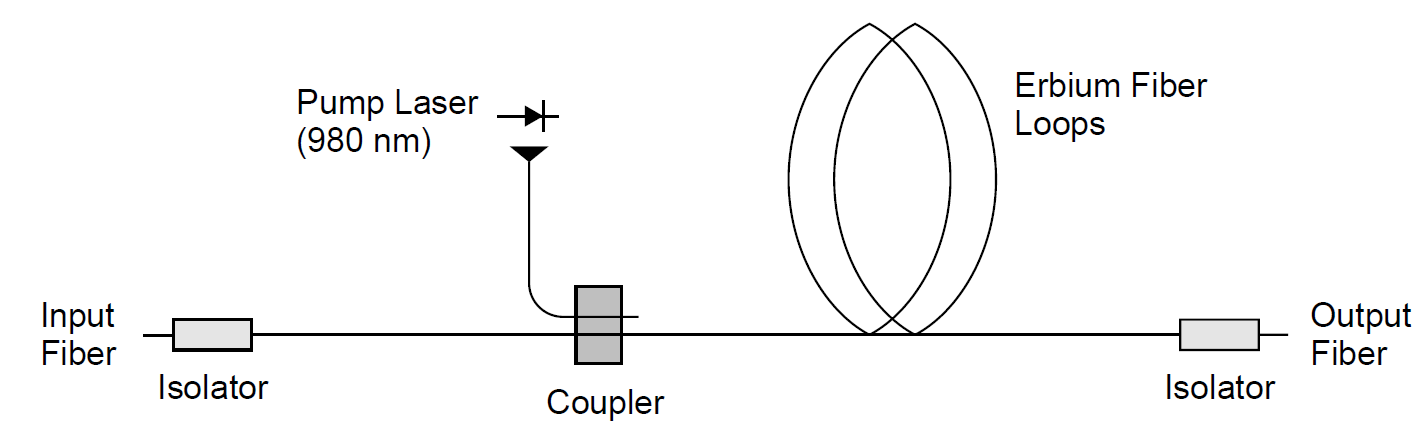
Figure 1.2. Fiber amplifier.

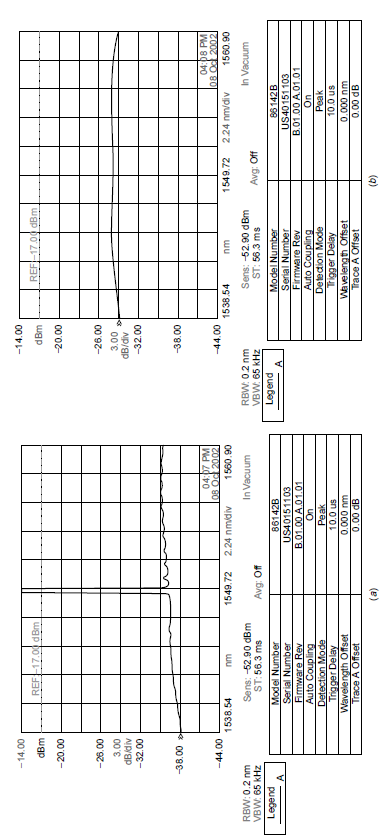
Figure 1.3. Fiber amplifier output.

          When a signal is fed into the fiber amplifier, the output consists of a large amount of signal seen as a spike at 1549 nm (the input signal highly amplified). The surprising part of this output, seen on the OSA in Figure 1.3(a), is the low background noise seen in the output around the spike at 1549 nm. When the amplifier is amplifying an input signal spontaneous emission is reduced drastically (in this case over 9 dB of reduction in noise in the output of the amplifier; the amplitude scale is identical in the two outputs shown in the figure, allowing comparison). When amplifying a signal (in this case a large signal which essentially saturates the amplifier), excited atoms of erbium which would, in the absence of a signal, emit spontaneously are coaxed into emitting coherent light; that is, they emit coherent light stimulated emission before they get a chance to emit light spontaneously, hence lowering the rate of spontaneous emission. This stimulated emission process (the key process by which this amplifier works) causes excited atoms to emit coherent light. Erbium, the species responsible for amplification here, has a relatively long spontaneous radiative lifetime in the upper lasing level, giving the process of stimulated emission a good probability of occurring before spontaneous emission occurs.