ATOMIC MODELS AND LIGHT EMISSION

The Rutherford Bohr atomic model was a huge step forward in explaining the mechanism of light emission and was based on experimental evidence. Rutherford performed experiments in which alpha particles (literally, helium nuclei consisting only of neutrons and protons) were scattered by atomic collisions. This demonstrated that atoms have a dense core (the nucleus) where positive charge is concentrated. On the wings of this discovery, Neils Bohr completed the model (called the Rutherford–Bohr model), which accounted for the emission spectra seen in hydrogen and other gases. The model postulates that electrons around an atom orbit in a number of possible energy states. In these discrete (allowed) states, electrons orbit the nucleus of the atom according to the laws of Newtonian mechanics. The angular momentum of these orbiting electrons is quantized and limited to a set of values, integer values called the quantum number, which represents which orbit the electron is in. Atoms do not radiate energy as long as they are fixed in that orbit. This application of Newtonian mechanics is not surprising, as it is analogous to the moon in high orbit around Earth. The only unusual part of this application was the fact that these orbits could take on only certain limited values (i.e., the fact that they were indeed quantized). The larger the quantum number n, the larger the orbit. Bohr postulated that the radius of an orbit was given by

  r = n²a₀    (1.1)

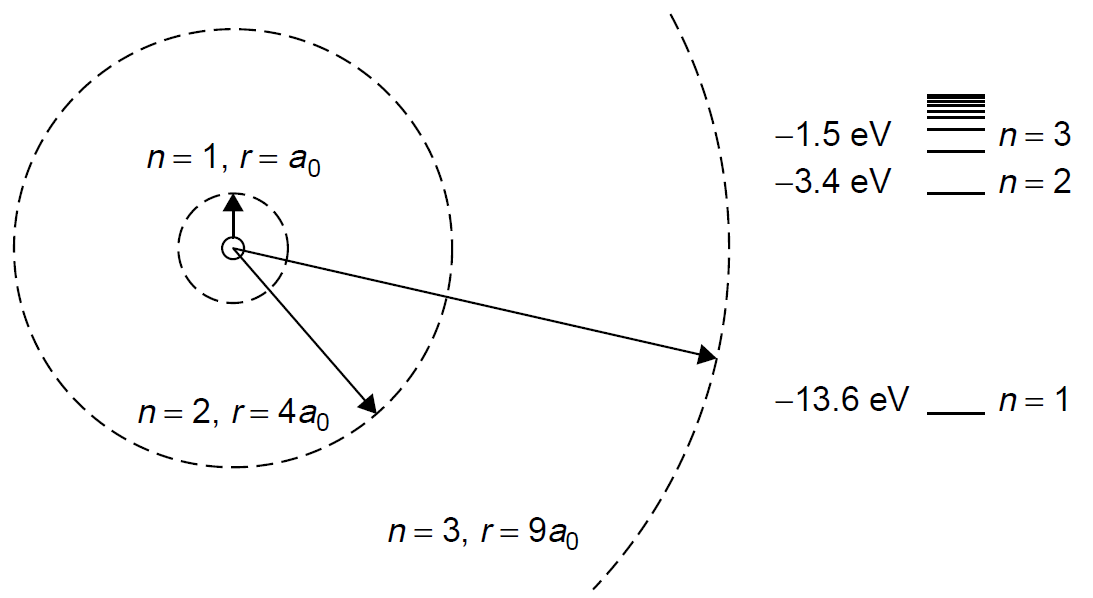
Figure 1.1. Hydrogen orbits and corresponding energy levels.

where n is the quantum number and a₀ is the Bohr radius (5.29 × 10^-11 m). The Bohr radius (a₀) is a figure that represents the radius of the smallest orbit. In practical terms, it is the highest energy that a bound electron (one orbiting around the nucleus) can have, which occurs at its closest approach to the nucleus. If we now consider an electron of very small mass to be orbiting a proton of much larger mass and use Coulomb’s law to determine the energy of the electron (which has a negative charge), classical kinematics allows calculation of the radii of orbits in the hydrogen atom. Newtonian mechanics can be applied to the orbit to render a figure for the energy of an electron in that particular orbit:

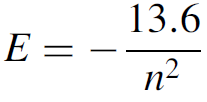
where E is the energy in eV. The energy is always negative since the frame of reference is that an unbound electron, one free of the hydrogen nucleus (but with no extra kinetic energy), has zero energy. When the energy levels for various quantum numbers are calculated, we find that electrons in the first Bohr orbit have an energy of 213.6 eV. As the quantum number increases, these levels get crowded closer together, as outlined in Figure 1.1, which shows for comparison the radius of the first three orbits of a hydrogen electron, as well as defined energy levels for the hydrogen atom. When an energy greater that 13.6 eV is supplied to a hydrogen atom in the ground state (i.e., the electron is in the first Bohr orbit, with n = 1), the electron will acquire so much energy that it is ejected from the atom altogether. The atom now becomes an ion and has an overall positive charge (the atom has become ionized). This is, incidentally, how the energy for the ground state (213.6 eV) is determined. Having defined energy levels in the atom, Bohr stated further that atoms may jump from one energy state to another (a quantum jump), corresponding to a change in orbit, and in doing so will emit radiation in the form of a photon. The photon will contain the energy difference between the initial, higher-energy state and the final, lower-energy state. This ensures conservation of energy, one of the founding laws of physics. The total energy of the process must remain unchanged, so that

E_photon = E_{upper level} - E_{lower level}

Recall that the emission spectrum of hydrogen consists of discrete lines, each of which can now be explained as corresponding with a jump or transition in the energy states of the atom (a change in orbit, if you will). In the case of the Balmer series, each line corresponds to an energy-level change which results in the final energy state being n = 2 (the second orbit). Higher-energy photons result from larger jumps, such as the violet line, which results from transitions from very high orbital states to the final n = 2 state. The red line has relatively little energy; it results from a relatively small jump between the n = 3 and n = 2 orbital states. The five visible lines of hydrogen may now be seen as a jump between a higher energy state with n = 3, 4, 5, 6, or 7 and a lower-energy state with n = 2. Mathematically, this can be determined by calculating the energy for each Bohr orbit and then the energy lost in a downward quantum jump. For example, consider the transition from n = 3 to n = 2 as depicted in Figure 1.2. The energy associated with each orbit is calculated to be -21.511 and -23.400 eV, respectively. When the transition occurs, the energy of the liberated photon will be equal to the difference in energy between these two levels, or 1.889 eV. This corresponds to a photon at a wavelength of 656.3 nm in the red. Applying the same calculation to the n = 4 to n = 2 transition yields a photon of 486.1 nm. In the latter case the jump is larger, so the energy lost to the photon is also larger. Transitions between energy levels do not have to end at n = 2 but can end at almost any level, such as n = 1 (the first orbit). These transitions have very high energies, being so close to the nucleus (from kinematics we know that low orbits close to the

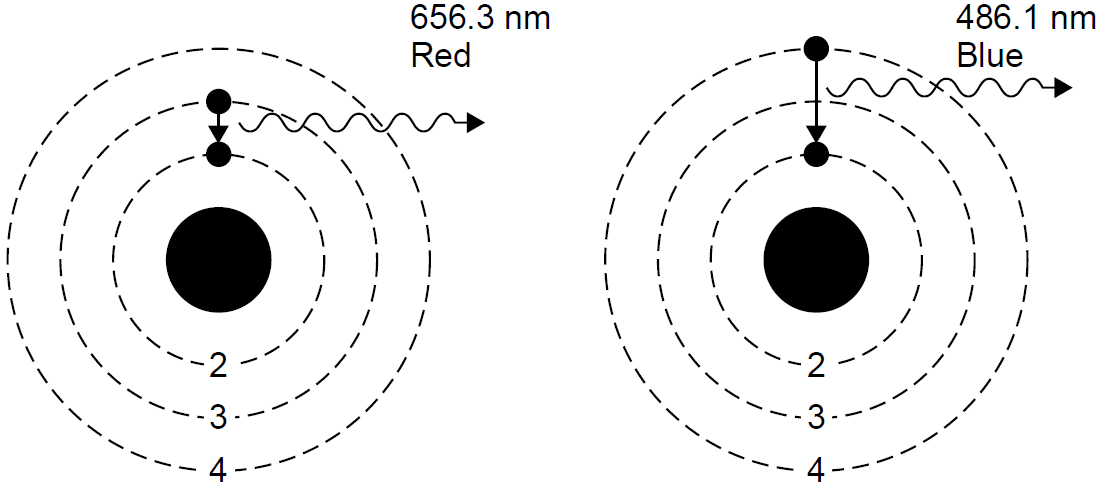
Figure 1.2. Photon emission in hydrogen.

center of mass have higher energies), so photons emitted in transitions to this final state of n = 1 also have high energies. These lines are observed in the ultraviolet and are called the Lyman series of lines. Other transitions end with n = 3 and have lower energy changes, so photons emitted are in the infrared (the Paschen series).