DETERMINING THE CRITICAL ANGLE
المؤلف:
S. Gibilisco
المصدر:
Physics Demystified
الجزء والصفحة:
505
8-11-2020
2464
DETERMINING THE CRITICAL ANGLE
Refer again to Fig. 1. The light passes from a medium having a relatively higher index of refraction r into a medium having a relatively lower index s. Therefore, r s. As angle x increases, angle y approaches 90°, and ray S gets closer to the boundary plane B. When x, the angle of incidence, gets large enough (somewhere between 0° and 90°), angle y reaches 90°, and ray S lies exactly in plane B. If angle x increases even more, ray R undergoes total internal reflection at the boundary plane B. Then the boundary acts like a mirror.
The critical angle is the largest angle of incidence that ray R can subtend relative to the normal N without being reflected internally. Let’s call this angle xc. The measure of the critical angle is the arcsine of the ratio of the indices of refraction:
xc = sin-1 (s/r)
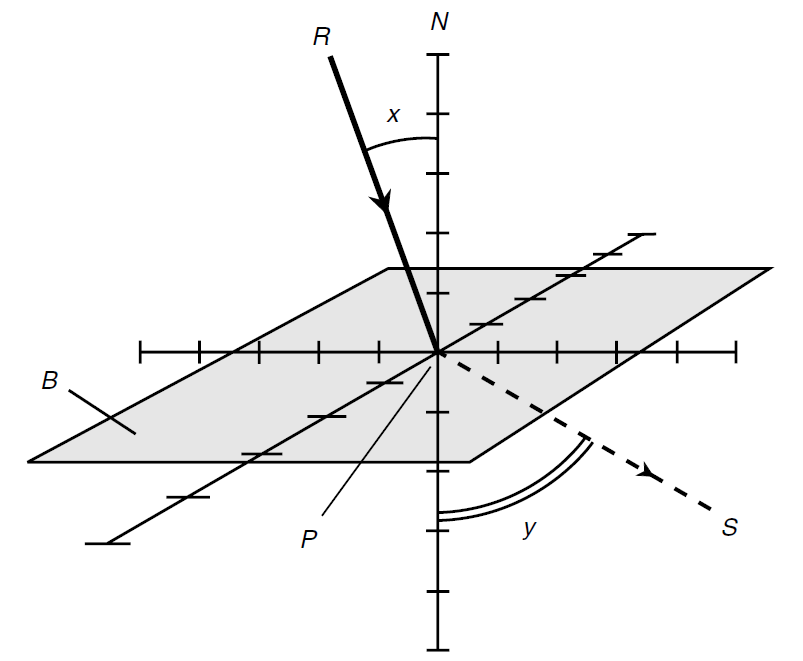
Fig. 1. A ray passing from a medium with a relatively higher refractive index to a medium with a relatively lower refractive index.
الاكثر قراءة في الضوء
اخر الاخبار
اخبار العتبة العباسية المقدسة
