BOLTZMANN DISTRIBUTION AND THERMAL EQUILIBRIUM

Every system has thermal energy. In the case of a gas, consider gas atoms confined to a cylinder. Thermal energy manifests itself as atoms colliding with each other and bouncing off the cylinder walls. It is these collisions of gas atoms with the cylinder walls that are manifested as gas pressure. In a solid, the thermal energy manifests itself as vibrations of the atoms making up the solid; when the vibrations are too much for the interatomic forces keeping the atoms in place, the atoms are no longer tied to a particular spot and start flowing past one another; this is what happens when a solid melts. Thermal energy also excites atoms (no matter what form they are in: gas, solid, or liquid), raising them to higher energy levels: The more thermal energy that is injected into a system (i.e., the higher the temperature), the more that higher energy levels will be populated. The resulting distribution of energy, describing the population of atoms at each energy level, is governed by Boltzmann’s law, one of the fundamental laws of thermodynamics. Boltzmann’s law predicts the population of atoms at a given energy level as follows:

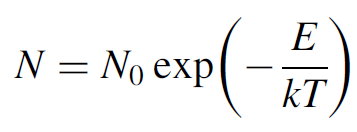 (1.1)

where N is the population of atoms at the given energy level, N₀ the population of atoms at ground state, E the energy above ground level in Joules, k is Boltzmann’s constant (1.38 × 10^-23 J/K), and T is the absolute temperature in Kelvin. This is to say that the law predicts an exponential drop in populations of atoms at higher energies. If we assume that a substance has an infinite number of energy levels (a continuum), the population at any given energy can be calculated using this law. The resulting distribution of energy for various energy levels is graphed in a generalized form in Figure 1.1. We can rewrite Boltzmann’s law as a ratio of N/N₀, allowing us to predict the distribution of atoms at any given energy level. Consider a generic substance at room temperature (293 K). In order to emit red light, we would need to excite atoms in the substance to 1.7 eV above ground (where an electron volt is equal to

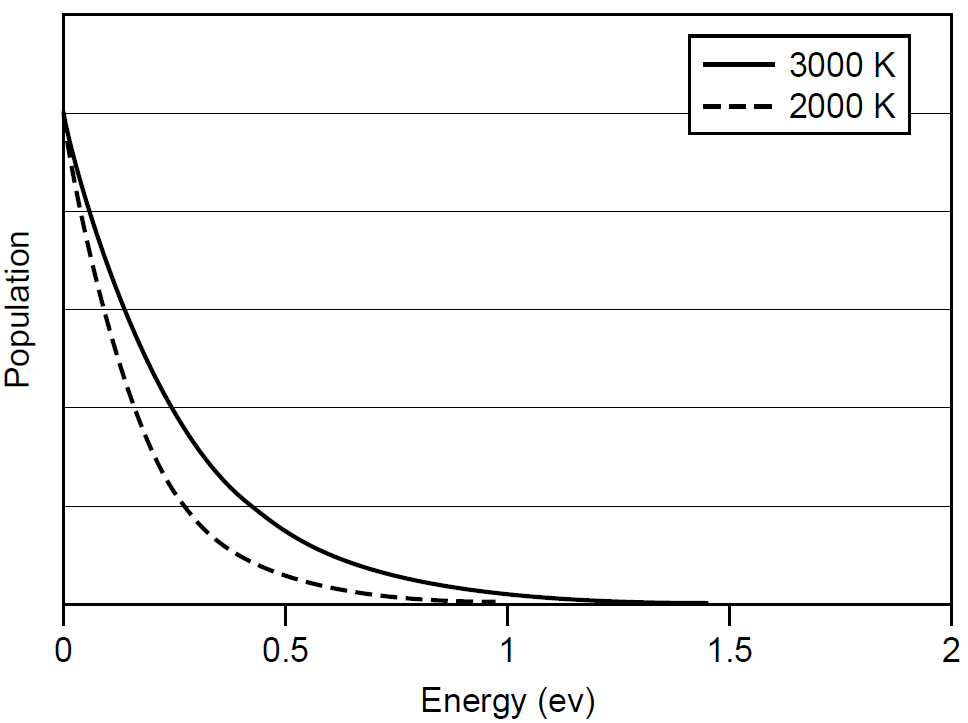
Figure 1.1. Generalized Boltzmann distribution of atomic energies.

1.602 × 10^-19 J of energy). The number of atoms at this higher-energy state is on the order of 10^-30! It is fair to say that there are essentially no atoms with energy this high at room temperature (and this energy level isn’t really very high at all; ions have much higher energies). Now, if the temperature is increased to, say, 5000 K, the population of atoms at this energy level increases to 2 × 10^-2 or 2%, a sizable concentration at this level which will lead to the emission of light when these atoms lose their energy and return to ground state. The experience of observing red-hot and white-hot objects such as a stove element or glowing metal shows us that anything heated to beyond 1000 K will emit light in the form of a glow. In a system such as we have described, it is assumed that there are no external sources of energy, so the population of atoms at any given energy level is governed solely by temperature. It is then said to be in thermal equilibrium. Examining the formula, we can see that if the temperature of the entire system were raised, the distribution would shift and more atoms would reach higher energies; however, the population of a lower level will always exceed that of a higher level. Higher temperatures result in increased populations of atoms at higher energy levels, and this results in larger energies. Light-producing transitions in such a substance will also have more energy, so more emitted photons from hotter objects will have more energy (and hence be shifted toward the blue region of the spectrum) than the photons emitted by cooler objects. It must also be noted that only at 0 K (absolute zero) will all atoms be at ground state (the lowest energy level).