


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 17-1-2016
التاريخ: 5-11-2020
التاريخ: 7-2-2021
التاريخ: 3-1-2017
|
القوة الدافعة الكهربائية الحركية
هناك طرق عديدة للحصول على ق. د. ك مستحثة. وبما اننا نعرف تغيرات الفيض خلال ملفات ساكنة بالدرجة الاولى ، وما ينشأ من ق. د. ك المستحثة. على أنه في بعض الاحيان تكون ق. د. ك المستحثة ناتجة عن حركة سلك خلال مجال مغناطيسي. وفي مثل هذه الحالات ، يكون من المناسب أكثر أن نشتق نتيجة لا تعتمد مباشرة على مفهوم تغير الفيض خلال عروة.
وسنبدأ بتناول التجربة البسيطة المبينة في الشكل (1) ، حيث ينزلق قضيب طول التقريبي l بسرعة V على طول سلكين متوازيين على شكل الحرف U يبدأ من m مروراً بكل من r و s ثم يصل إلى n ويلاحظ أن القضيب إلى اليمين ازدادت مساحة هذه العروة.
سنفترض الآن أن هناك مجالاً مغناطيسياً B يتجه خارجاً من الصفحة في هذه المنطقة. ومع حركة القضيب يزداد الفيض الذي يخترق المساحة لأن المساحة نفسها تزداد ، ولهذا تستحدث ق. د. ك في العروة. ولكي نسحب هذه القوة الدافعة الكهربية فإننا نلاحظ أن القضيب يتحرك مسافة مقدارها vΔt في زمن قدره Δt ، أي أن مساحة العروة تزداد بما قيمته ΔA = l (vΔt)، وهي عبارة عن الجزء المظلل في الشكل. ومقدار التغير في الفيض هو
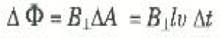
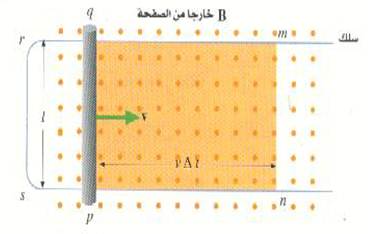
الشكل ((1: عندما يتحرك القضيب نحو اليمين فإن المساحة المحددة بالدائرة pqrsp تزداد مما يؤدي إلى زيادة الفيض المغناطيسي خلال هذه الدائرة. وطبقاً لقانون لنز ، يؤدي هذا إلى ق. د. ك مستحثة في الدائرة.
ومن ثم يكون مقدار د. ق. ك المستحثة في العروة طبقاً لقانون فاراداي هو
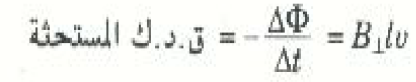
وعليك التأكد من أن هذه القوة الدافعة الكهربية المستحثة سوف تنشى تياراً يمر في الدائرة في اتجاه حركة عقارب الساعة.
وهناك وسيلة أخرى لتحليل هذا الموقف. اعتبر شحنة موجبة q بداخل القضيب المتحرك كما في الشكل ((2. وتتعرض هذه الشحنة بفضل حركتها بسرعة v خلال B لقوة مقدارها qvB┴. والمجال الكلي في هذه الحالة متعامد مع سرعة الشحنة ولذا يكون B = B┴ ومنها نستنتج أن:

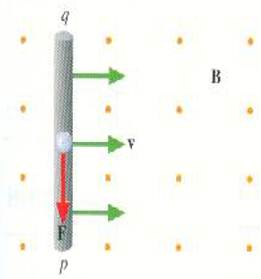
الشكل (:(2 القوة المؤثرة على شحنة موجية داخل قضيب موصل وتتحرك عمودية على مجال مغناطيسي.
إذا استعملت قاعدة اليد اليمنى فإنك تدرك أن القوة المؤثرة على q تتجه من النقطة q إلى النقطة p على طول القضيب. ولهذا*
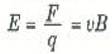
وإذا تذكرنا أن فرق الجهد الكهربي بين النقطتين مساو للشغل المبذول في نقل شحنة اختبار قيمتها الوحدة من نقطة إلى أخرى ، فسنصل إلى أن فرق الجهد من P إلى q يفضل المجال الكهربي E هو
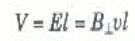
يلاحظ هنا ان هذا المقدار مساو تماماً للقوة الدافعة الكهربية المستحثة في العروة والتي أوجدناها باستخدام قانون فاراداي. ثم إن المجال الكهربي المستحث بحركة الشحنة يسبب مرور تيار في اتجاه حركة عقارب الساعة في العروة ، وهو أيضاً نفس الاتجاه الذي وجدناه من قانون فاراداي. وفيما يلي تلخيص للنتائج التي يحصلنا عليها:
عندما يتحرك سلك ( أو قضيب) طوله l بسرعة v عمودياً على كل من المجال المغناطيس B وطوله نفسه فإن ق. د. ك تستحث عبر طول هذا السلك:
(1) 
وهي ما يطلق عليها ق. د. ك الحركية. ويلاحظ أنه من غير الضروري وجود عروة أو دائرة كاملة لظهور ق. د. ك مستحثة بين طرفي القضيب . وفي الحالة الأكثر عمودية عندما لا تكون B ، v والسلك متبادلة التعامد فإن مركبتي B و v المتعامدتين مع بعضهما ومع السلك هما اللتان تستعملان.
_____________________________
(*) وإذا شئنا التحديد فإن قيمة E هذه لا تنطبق إلا في مناط إسناد يتحرك مع الشحنة.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
ضمن أسبوع الإرشاد النفسي.. جامعة العميد تُقيم أنشطةً ثقافية وتطويرية لطلبتها
|
|
|