
 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء| The Puzzle of Information Conservation in Black Hole Environments |
|
|
|
Read More
Date: 6-2-2017
Date: 24-1-2017
Date: 22-12-2015
|
The Puzzle of Information Conservation in Black Hole Environments
In 1976 Hawking raised the question of whether information is lost in the process of formation and evaporation of black holes. By information loss, Hawking did not mean the practical loss of information such as would occur in the bomb. He meant that in a fine grained sense, information would be lost. In other words, the first of the laws of nature described in the Introduction would be violated. The argument was simple and persuasive. It was based on the only available tool of that time, namely local quantum field theory in the fixed background of a black hole. Although Hawking's conclusion is undoubtedly wrong, it played a central role in replacing the old ideas of locality with a new paradigm.
As we have already seen, quantum field theory has a serious defect when it comes to describing systems with horizons. It gives rise to an infinite entropy density on the horizon, instead of the correct Bekenstein–Hawking value of c3/4Gh.As we will see, quantum field theory must be replaced with an entirely new paradigm in which the concept of locality is radically altered.
To state the problem, let's begin with a black hole that has been formed during a collapse. The Penrose diagram is shown in Figure 1.1. Following Hawking, we think of the geometry as a background on which we can formulate quantum field theory. Let us concentrate on a theory of massless particles.
According to the principles of quantum mechanics, the evolution of an initial state |ψin> is governed by a unitary S-matrix, so that the final state is given by
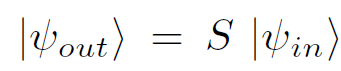 (1.1)
(1.1)
One way of stating the principle of information conservation is through the unitarity of S. The point is that a unitary matrix has an inverse, so that
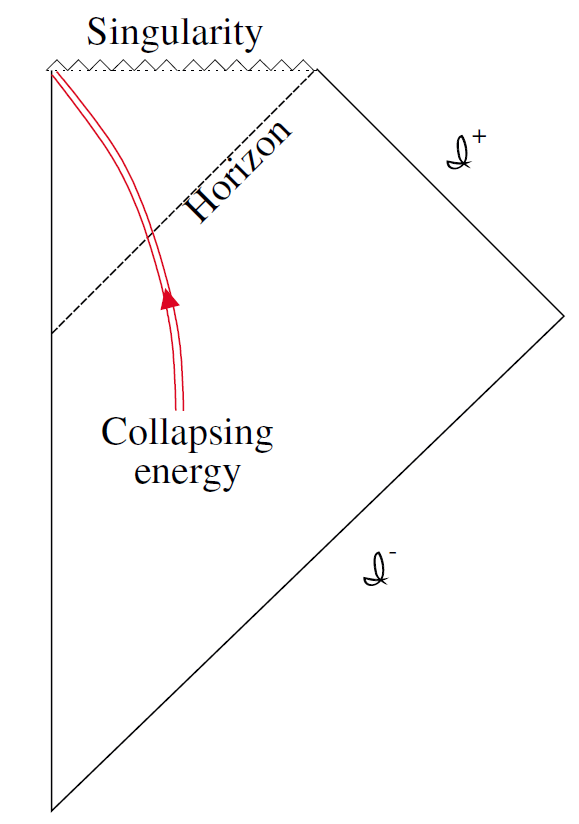
Fig. 1.1. Penrose diagram of black hole formed by collapse.
in principle the initial state can be recovered from the final state
 (1.2)
(1.2)
Now let us consider the S-matrix in a black hole background. The Hilbert space of initial states Hin is clearly associated with quanta coming in from  −.These incoming particles will interact and scatter by means of Feynman diagrams in the black hole background. It is evident from Figure 1.2 that some of the final particles will escape to
−.These incoming particles will interact and scatter by means of Feynman diagrams in the black hole background. It is evident from Figure 1.2 that some of the final particles will escape to 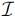 + and some will be lost behind the horizon. Evidently the final Hilbert space, Hout is a tensor product of the states on I+ and those at the singularity S. Thus
+ and some will be lost behind the horizon. Evidently the final Hilbert space, Hout is a tensor product of the states on I+ and those at the singularity S. Thus
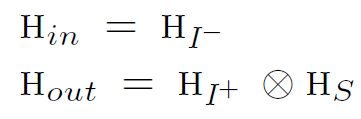 (1.3)
(1.3)
In arguing that the final Hilbert space is a tensor product, Hawking
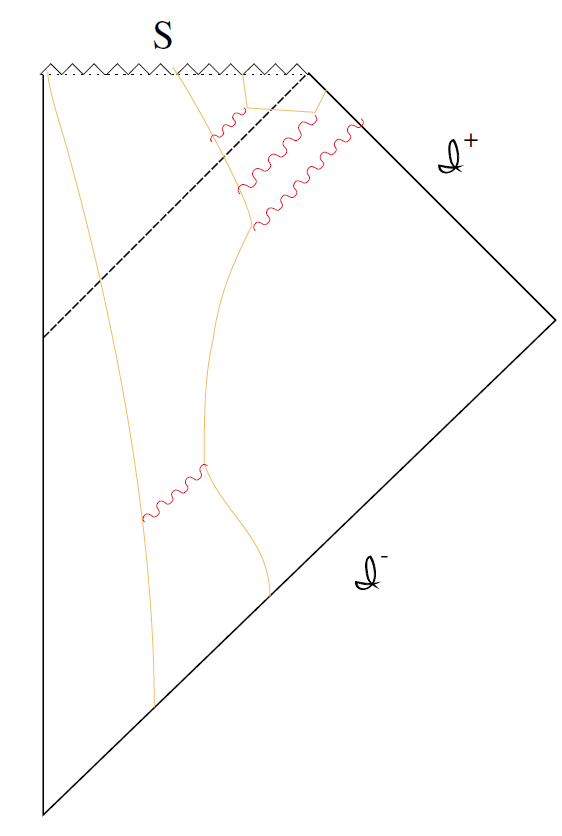
Fig. 1.2. Feynman diagrams in black hole background.
relied on an important property of quantum field theory: locality. Since every point on the singularity S is space-like relative to every point on 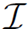 +, the operators on S all commute with those on
+, the operators on S all commute with those on  +. This was central to Hawking's analysis.
+. This was central to Hawking's analysis.
Now suppose that the final state is given by an S-matrix which connects Hin and Hout as in equation 1.1. Let us consider the description of the final state from the viewpoint of the observers at  +. Since they have no access to S, all experiments on the outgoing particles are described by a density matrix
+. Since they have no access to S, all experiments on the outgoing particles are described by a density matrix
 (1.4)
(1.4)
where Trsingularity means a trace over the states on the singularity. Thus, in general the observer external to the black hole will see a state characterized by a density matrix.
A simple example might involve a pair of correlated particles which are thrown in from 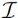 −. By correlated, we mean that the two particles wave function is entangled. If one particle ends up on S and the other ends up on
−. By correlated, we mean that the two particles wave function is entangled. If one particle ends up on S and the other ends up on 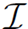 +, then the final state will be entangled. In this case the state on
+, then the final state will be entangled. In this case the state on 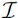 + will not be pure.
+ will not be pure.
Hawking went on to make arguments that the purity of the state would not be restored if the black hole evaporated. In fact, the only possibilities would seem to be that either information is lost during the entire process of formation and evaporation, or the information is restored to the outside world at the very end of the evaporation process, when the singularity is “exposed” at Planckian temperature.
However, the maximum amount of information that can be hidden in a system is its entropy. Once the entropy of the black hole has evaporated past 1/2 its original value, it must begin to come out in the emitted radiation. This is a fundamental law of quantum mechanics. By the time the black hole has small mass and entropy, the entanglement entropy of the radiation cannot be larger than the black hole's remaining entropy. Thus, even if all information were emitted at the very end of the evaporation process, a law of nature would be violated from the viewpoint of the external observer. The situation is even worse if the information is not emitted at all.
A final possibility that was advocated by some authors is that black holes never completely evaporate. Instead they end their lives as stable Planck-mass remnants that contain all the lost information. Obvious such remnants would have to have an enormous, or even infinite entropy. Such remnants would be extremely pathological, and we will not pursue that line further.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
العتبة الحسينية تطلق فعاليات المخيم القرآني الثالث في جامعة البصرة
|
|
|