


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 5-7-2016
التاريخ: 2024-01-06
التاريخ: 6-2-2021
التاريخ: 13-7-2017
|
Finally, we should emphasize that not only do modes exist for complicated continuous systems, but also for very simple mechanical systems. A good example is the system of two coupled pendulums discussed in the preceding chapter. In that chapter it was shown that the motion could be analyzed as a superposition of two harmonic motions with different frequencies. So even this system can be analyzed in terms of harmonic motions or modes. The string has an infinite number of modes and the two-dimensional surface also has an infinite number of modes. In a sense it is a double infinity, if we know how to count infinities. But a simple mechanical thing which has only two degrees of freedom, and requires only two variables to describe it, has only two modes.
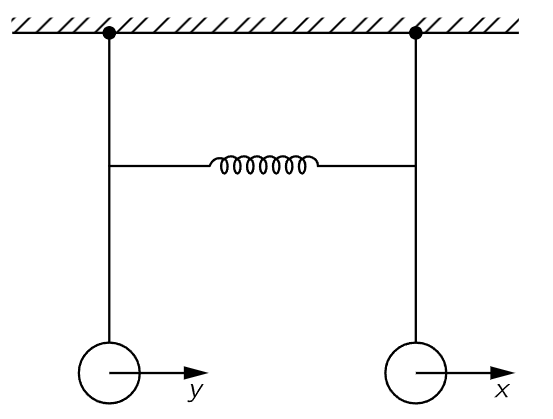
Fig. 49–5. Two coupled pendulums.
Let us make a mathematical analysis of these two modes for the case where the pendulums are of equal length. Let the displacement of one be x, and the displacement of the other be y, as shown in Fig. 49–5. Without a spring, the force on the first mass is proportional to the displacement of that mass, because of gravity. There would be, if there were no spring, a certain natural frequency ω0 for this one alone. The equation of motion without a spring would be
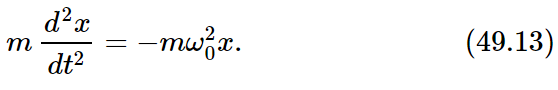
The other pendulum would swing in the same way if there were no spring. In addition to the force of restoration due to gravitation, there is an additional force pulling the first mass. That force depends upon the excess distance of x over y and is proportional to that difference, so it is some constant which depends on the geometry, times (x−y). The same force in reverse sense acts on the second mass. The equations of motion that have to be solved are therefore
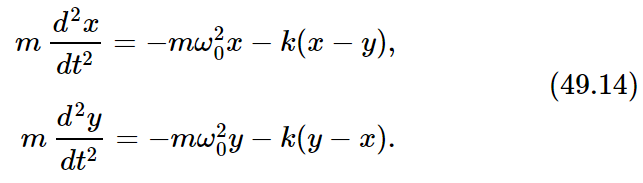
In order to find a motion in which both of the masses move at the same frequency, we must determine how much each mass moves. In other words, pendulum x and pendulum y will oscillate at the same frequency, but their amplitudes must have certain values, A and B, whose relation is fixed. Let us try this solution:
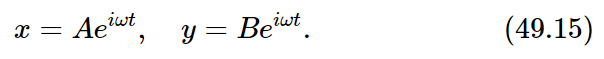
If these are substituted in Eqs. (49.14) and similar terms are collected, the results are
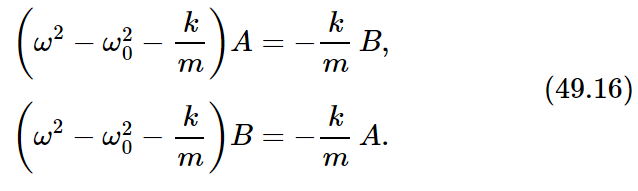
The equations as written have had the common factor eiωt removed and have been divided by m.
Now we see that we have two equations for what looks like two unknowns. But there really are not two unknowns, because the whole size of the motion is something that we cannot determine from these equations. The above equations can determine only the ratio of A to B, but they must both give the same ratio. The necessity for both of these equations to be consistent is a requirement that the frequency be something very special.
In this particular case this can be worked out rather easily. If the two equations are multiplied together, the result is

The term AB can be removed from both sides unless A and B are zero, which means there is no motion at all. If there is motion, then the other terms must be equal, giving a quadratic equation to solve. The result is that there are two possible frequencies:
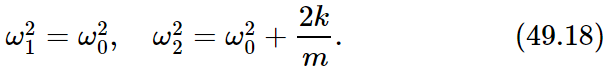
Furthermore, if these values of frequency are substituted back into Eq. (49.16), we find that for the first frequency A=B, and for the second frequency A=−B. These are the “mode shapes,” as can be readily verified by experiment.
It is clear that in the first mode, where A=B, the spring is never stretched, and both masses oscillate at the frequency ω0, as though the spring were absent. In the other solution, where A=−B, the spring contributes a restoring force and raises the frequency. A more interesting case results if the pendulums have different lengths. The analysis is very similar to that given above, and is left as an exercise for the reader.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|