
Rotation
 المؤلف:
Richard Fitzpatrick
المؤلف:
Richard Fitzpatrick
 المصدر:
Classical Electromagnetism
المصدر:
Classical Electromagnetism
 الجزء والصفحة:
p 15
الجزء والصفحة:
p 15
 13-7-2017
13-7-2017
 2561
2561
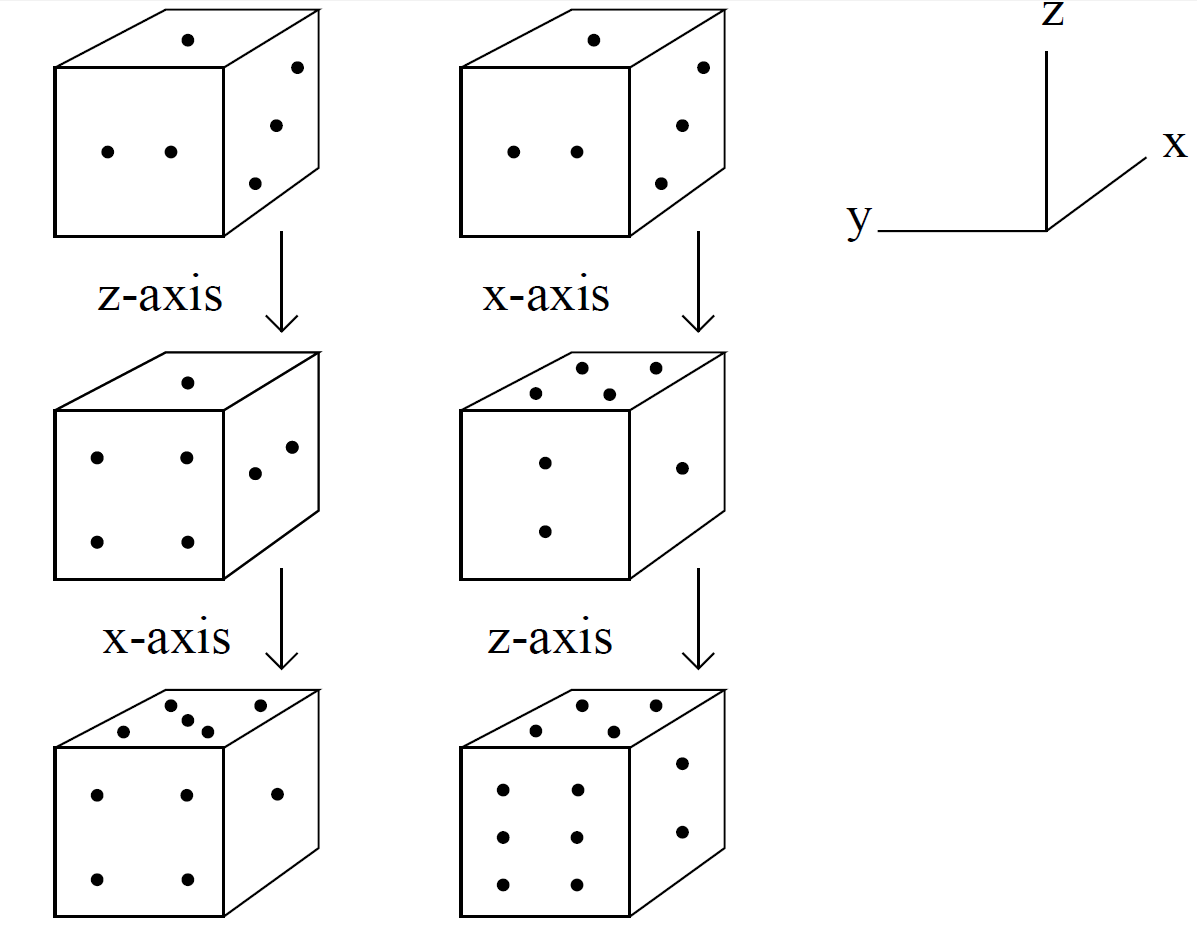
Let us try to define a rotation vector θ whose magnitude is the angle of the rotation, θ, and whose direction is the axis of the rotation, in the sense determined by the right-hand grip rule. Is this a good vector? The short answer is, no. The problem is that the addition of rotations is not commutative, whereas vector addition is. The diagram shows the effect of applying two successive 90o rotations, one about x-axis, and the other about the z-axis, to a six-sided die. In the left-hand case the z-rotation is applied before the x-rotation, and vice versa in the right-hand case. It can be seen that the die ends up in two completely different states. Clearly, the z-rotation plus the x-rotation does not equal the x-rotation plus the z-rotation. This non-commuting algebra cannot be represented by vectors. So, although rotations have a well defined magnitude and direction they are not vector quantities. But, this is not quite the end of the story. Suppose that we take a general
vector a and rotate it about the z-axis by a small angle δθz. This is equivalent to rotating the basis about the z-axis by -δθz. We have
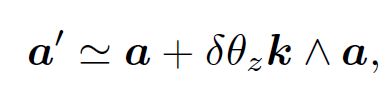 (1.1)
(1.1)
where use has been made of the small angle expansions sin θ  θ and cos θ
θ and cos θ  1. The above equation can easily be generalized to allow small rotations about the x- and y-axes by δθx and δθy, respectively. We find that
1. The above equation can easily be generalized to allow small rotations about the x- and y-axes by δθx and δθy, respectively. We find that
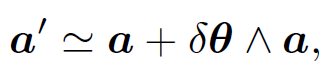 (1.2)
(1.2)
where
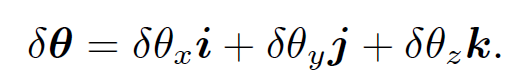 (1.3)
(1.3)
Clearly, we can define a rotation vector δθ, but it only works for small angle rotations (i.e., sufficiently small that the small angle expansions of sine and cosine are good). According to the above equation, a small z-rotation plus a small x-rotation is (approximately) equal to the two rotations applied in the opposite order. The fact that infinitesimal rotation is a vector implies that angular velocity,
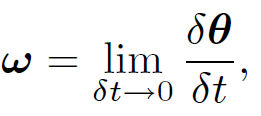 (1.4)
(1.4)
must be a vector as well. If aʹ is interpreted as a(t + δt) in the above equation then it is clear that the equation of motion of a vector precessing about the origin with angular velocity 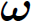 is
is
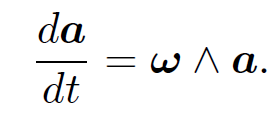 (1.5)
(1.5)
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


