المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | اقتران أسي Exponential Function |
 31288
 02:58 صباحاً
التاريخ: 28-10-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 29-30|
أقرأ أيضاً
التاريخ: 29-10-2015
1161
التاريخ: 16-12-2015
1990
التاريخ: 18-11-2015
2838
التاريخ: 22-11-2015
1457
|
والاقتران الأسي من الاقترانات المتسامية ــ الغير جبرية ــ ويمثل ارتباط بين عناصر المتغير س وعناصر المتغير ص – ق(س) وعلى الصورة ق(س) = أس حيث أ عدد حقيقي وموجب ولا يساوي الواحد الصحيح وإلا انقلب هذه الاقتران إلى اقتران ثابت كون ق(س) = أس = 1 مهما كانت قيم س .
وباختصار شديد هو اقتران المتغير فيه كأس وتمثيله البياني كما في الشكلين التاليين:
عندما أ>1
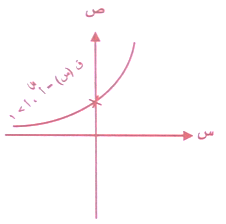
عندما أ<1
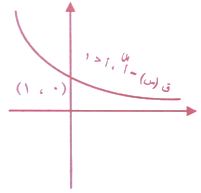
والملاحظة أن كلاً من الاقترانيين ق(س) = سس أ , أ<1, ق(س) = سس أ , أ>1 يمران بالنقطة (0,1) لأنه عندما س = صفر فإن ق(س) = أ = 1 مهما كانت قيمة أ .
والعلاقة بين بياني الاقترانيين ومن الشكل تقول :
أن بيان الاقتران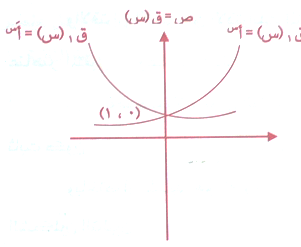
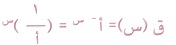
انعكاس لبيان الاقتران ق(س)=أس في محور الصادات ما دام أ عدداً موجباً لا يساوي الواحد الصحيح كماا ورد بالتعريف ومن الملاحظ أيضاً ان مجال الاقتران الأسي هو الاعداد الحقيقية ح (الموجبة والصفر والسالبة) ولكن مداه فهي الاعداد الحقيقية الموجبة ح+ فقط , كون بيانه فوق محور السينات فقط ولا يقطعه أبداً.
|
|
|
|
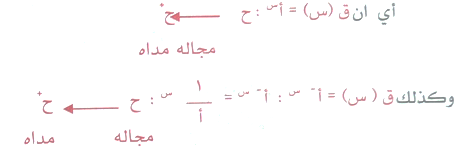
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|
