Cayley Graph

Let  be a group, and let  be a set of group elements such that the identity element . The Cayley graph associated with  is then defined as the directed graph having one vertex associated with each group element and directed edges  whenever . The Cayley graph may depend on the choice of a generating set, and is connected iff  generates  (i.e., the set  are group generators of ).

Care is needed since the term "Cayley graph" is also used when  is implicitly understood to be a set of generators for the group, in which case the graph is always connected (but in general, still dependent on the choice of generators). This sort of Cayley graph of a group  may be computed in the Wolfram Language using CayleyGraph[G], where the generators used are those returned by GroupGenerators[G].

To complicate matters further, undirected versions of proper directed Cayley graphs are also known as Cayley graphs.

An undirected Cayley graph of a particular generating set of the alternating group  is sometimes known as a alternating group graph. The Cayley graph of the cyclic group  is the cycle graph , and of the dihedral group  is the prism graph . Other classes of graphs that are Cayley graphs are circulant graphs (connected if requiring a generating set; possibly disconnected if not), cube connected cycles, Hamming graphs, and hypercube graphs.

A directed graph Cayley graph has the same edge multiplicity for each node. A (directed or undirected) Cayley graph is always vertex-transitive, but the converse need not hold. However, a large fraction of small vertex-transitive graphs are Cayley graphs (McKay and Royle 1990).

Royle maintains a list of not-necessarily-connected vertex-transitive graphs with Cayley or non-Cayley designations up to 31 vertices and although the values for 27, 28 and 30 vertices have not been independently verified (though an error in the groups can only affect the graphs if somehow a minimal transitive group has been omitted, so errors are unlikely). The numbers of not-necessarily-connected Cayley graphs on , 2, ... nodes are 1, 2, 2, 4, 3, 8, 4, 14, 9, 20, 8, 74, ... (OEIS A185959; McKay and Royle 1990, McKay and Praeger 1994), and the numbers of nodes on which non-Cayley vertex-transitive graphs exist are 10, 15, 16, 18, 20, 24, 26, 28, 30, ....

The smallest vertex-transitive non-Cayley graph is the Petersen graph  (McKay and Praeger 1994) and the smallest disconnected vertex-transitive non-Cayley graph is two copies of .

Cayley graphs can be generated by starting with a set of generator permutations  (which does not include the identity permutation) and mutually permuting elements until no new permutations are reached. This produces a set  that is closed under permutations of elements. Connecting each pair of permutations  with an edge if  for some  then gives a Cayley graph.

The only groups that can give planar Cayley graphs are exactly , , , , , and , as proved by Maschke (1896).

The following table lists some graphs that are undirected versions of Cayley graphs generated by small numbers of small permutations.

graph	generators
16-cell graph	1,2,4,3, 2,1,3,4, 2,1,4,3, 3,4,1,2, 3,4,2,1
circulant graph	1,2,3,5,4, 1,2,4,3,5, 2,1,3,5,4, 2,1,5,4,3
complete bipartite graph	1,2,4,3, 2,1,3,4, 3,4,2,1
	1,2,4,3, 2,1,3,4, 3,4,1,2, 4,3,2,1
	1,2,4,5,6,3, 2,1,4,5,6,3
complete graph	1,3,2, 2,1,3, 2,3,1, 3,2,1
	1,2,4,3, 1,3,2,4, 1,3,4,2, 1,4,3,2
	1,2,4,3, 1,3,2,4, 1,3,4,2, 1,4,2,3, 1,4,3,2
cubical graph	1,2,4,3, 3,4,2,1
	1,2,4,3, 2,1,3,4, 3,4,1,2
	1,2,3,5,4, 1,4,5,3,2
cubic symmetric graph	1,2,4,3, 1,3,2,4, 3,2,1,4
	1,2,3,4,6,5, 2,5,4,6,3,1
cubic symmetric graph	1,3,2,5,4, 2,1,4,3,5, 4,5,3,1,2
cubic vertex-transitive graph Ct19	1,2,3,4,6,5, 1,2,4,3,6,5, 5,6,3,4,1,2
cubic vertex-transitive graph Ct23	1,2,3,4,6,5, 2,3,1,5,6,4
cubic vertex-transitive graph Ct28	1,3,2,5,4, 2,3,4,1,5
cubic vertex-transitive graph Ct37	1,2,4,3, 1,3,2,4,3,4,1,2
cubic vertex-transitive graph Ct38	1,2,3,4,5,7,6, 2,3,1,6,7,4,5
cubic vertex-transitive graph Ct41	1,2,4,3, 1,3,2,4,2,1,4,3
cubic vertex-transitive graph Ct42	1,2,3,4,5,7,6, 2,3,4,1,6,5,7
cuboctahedral graph	1,3,4,2, 2,3,1,4
	1,3,4,2, 1,4,2,3, 2,3,1,4
	1,3,4,2, 1,4,2,3, 2,3,1,4, 3,1,2,4
	1,2,4,5,3, 1,3,4,2,5
5-cycle graph	2,3,4,5,1, 5,1,2,3,4
6-cycle graph	1,3,2, 2,1,3
	1,2,4,3, 1,3,2,4
	1,2,3,5,4, 1,2,4,3,5
8-cycle graph	1,2,4,3, 3,4,1,2
	1,2,3,5,4, 1,4,5,2,3
10-cycle graph	1,3,2,5,4, 2,1,4,3,5
12-cycle graph	1,2,3,5,4, 2,1,4,3,5
Franklin graph	1,2,3,5,4, 1,2,4,3,5, 2,1,3,5,4
	1,2,3,4,5,7,6, 1,2,3,4,6,5,7, 1,2,4,3,5,7,6
great rhombicuboctahedral graph	1,2,3,4,5,7,6, 1,2,3,4,6,5,7, 1,3,2,5,4,7,6
icosahedral graph	1,3,4,2, 2,1,4,3, 2,3,1,4
	1,3,4,2, 1,4,2,3, 2,1,4,3, 2,3,1,4
	1,3,4,2, 1,4,2,3, 2,1,4,3, 2,3,1,4, 3,1,2,4
4-Möbius ladder	1,2,4,3, 2,1,4,3, 3,4,1,2
octahedral graph	1,3,2, 2,1,3, 2,3,1
	1,2,4,3, 1,3,2,4, 1,3,4,2
	1,2,4,3, 1,3,2,4, 1,3,4,2, 1,4,2,3
	1,2,4,5,3, 2,1,4,5,3
	1,2,4,5,3, 2,1,4,5,3
Pappus graph	1,2,3,4,6,5, 2,3,1,5,4,6
2-path graph	2,1
	1,3,2
pentatope graph	2,3,4,5,1, 3,4,5,1,2
5-prism graph	1,3,2,5,4, 2,4,1,5,3
	1,3,2,5,4, 2,4,1,5,3
6-prism graph	1,2,3,5,4, 2,1,4,5,3
	1,2,3,5,4, 2,1,4,5,3
small rhombicosidodecahedral graph	1,2,4,5,3, 3,4,2,5,1
small rhombicuboctahedral graph	1,3,4,2, 2,3,4,1
	1,3,4,2, 1,4,2,3, 2,3,4,1
	1,3,4,2, 1,4,2,3, 2,3,4,1, 4,1,2,3
	1,2,4,5,3, 1,3,4,5,2
snub cubical graph	1,2,4,3, 2,3,1,4, 2,3,4,1
	1,2,4,3, 2,3,1,4, 2,3,4,1, 3,1,2,4
	1,2,4,3, 2,3,1,4, 2,3,4,1, 3,1,2,4, 4,1,2,3
square antiprism graph	1,2,4,3, 3,4,1,2, 3,4,2,1
	1,2,4,3, 3,4,1,2, 3,4,2,1, 4,3,1,2
square graph	1,2,4,3, 2,1,3,4
	1,2,3,5,4, 1,3,2,4,5
tesseract graph	1,2,3,4,6,5, 1,2,4,3,5,6, 3,4,2,1,5,6
tetrahedral graph	2,1,4,3, 3,4,2,1
	1,2,4,3, 2,1,3,4, 2,1,4,3
	1,3,2,5,4, 1,4,5,3,2
triangle graph	2,3,1
	1,3,4,2, 1,4,2,3
	1,2,4,5,3, 1,2,5,3,4
triangular prism graph	1,3,2, 2,3,1
	1,2,4,3, 1,3,4,2
	1,2,4,3, 1,3,4,2, 1,4,2,3
	1,2,3,5,4, 1,2,4,5,3
truncated cubical graph	1,2,4,3, 2,3,1,4
	1,2,4,3, 2,3,1,4, 3,1,2,4
	1,2,3,5,4, 1,3,4,2,5
truncated dodecahedral graph	1,2,4,5,3, 3,4,1,2,5
truncated icosahedral graph	1,3,2,5,4, 2,3,4,5,1
truncated octahedral graph	1,2,4,3, 2,3,4,1
	1,2,4,3, 1,3,2,4, 2,1,3,4
	1,2,3,5,4, 1,3,4,5,2
truncated tetrahedral graph	1,3,4,2, 2,1,4,3
	1,3,4,2, 1,4,2,3, 2,1,4,3
	1,2,4,5,3, 1,3,2,5,4
utility graph	1,3,2, 2,1,3, 3,2,1
	1,2,4,3, 1,3,2,4, 1,4,3,2
	1,2,3,5,4, 2,3,1,5,4
	1,2,3,5,4, 2,3,1,5,4

For example, the dihedral group  is a permutation group on 14 elements that can be generated by two elements corresponding to a reversal and a rotation, respectively. Therefore, any two such elements give a connected Cayley graph that has 14 nodes and 28 edges. The left figure above shows the Cayley graph for the choice of generators given by (7, 1, 2, 3, 4, 5, 6) and (7, 6, 5, 4, 3, 2, 1), with reversals shown in red and rotations in blue. Any two elements corresponding to a rotation only with give a disconnected graph, and there are exactly 15 pairs of such elements since there are  ways to pick two elements from a six possible rotations. (Here, the number 6 appears instead of 7 since the unit element may not be a member of the subset giving the Cayley graph.) The right figure shows the Cayley graph for  generated by the elements (7, 1, 2, 3, 4, 5, 6) and (6, 7, 1, 2, 3, 4, 5), which is disconnected since these elements do not generate the group (in particular, without a flip, there is no way for permutations with positive order to switch to a negative order; hence two independent rings are obtained).

The figure above shows the Cayley graph for the alternating group  using the elements (2, 1, 4, 3) and (2, 3, 1, 4) as generators, which is a directed form of the truncated tetrahedral graph.

If three vertices of the complete graph  are covered with differently colored stones and any stone may be moved to the empty vertex, then the graph of all positions forms a Cayley graph with edges indicating neighboring positions (left figure). This corresponds to the Cayley graph of the symmetric group  using the elements (2, 1, 3, 4), (3, 2, 1, 4), and (4, 2, 3, 1) as generators. It turns out that this graph is a directed version of the unique cubic symmetric graph on 24 vertices (right figure).

Royle has constructed all cubic Cayley graphs up to 1000 vertices, excluding those on 512 and 768 vertices.

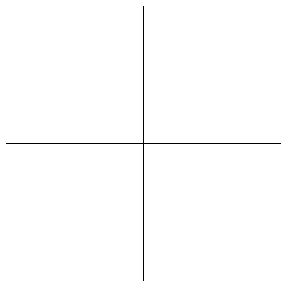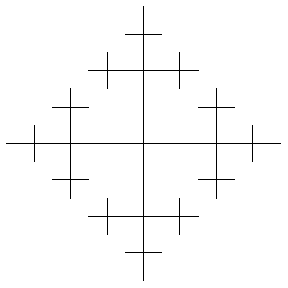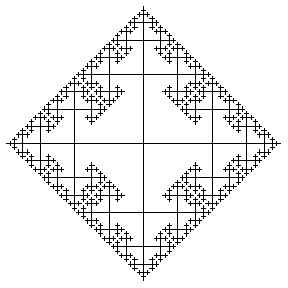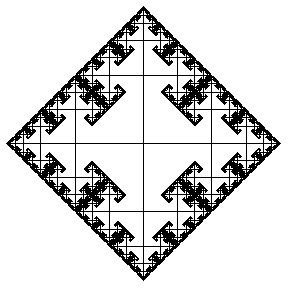
The Cayley graphs of infinite groups provide interesting geometries. For example, the Cayley graphs of the free group on two generators are illustrated above (drawn out to successive levels), representing horizontal and vertical displacement respectively. Each new edge is drawn at half the size to give fractal images.

REFERENCES

Holton, D. A. and Sheehan, J. The Petersen Graph. Cambridge, England: Cambridge University Press, pp. 292-293, 1993.

Maschke, H. "The Representation of Finite Groups." Amer. J. Math. 16, 156-194, 1896.

McKay, B. D. and Praeger, C. E. "Vertex-Transitive Graphs Which Are Not Cayley Graphs. I." J. Austral. Math. Soc. Ser. A 56, 53-63, 1994.

McKay, B. D. and Royle, G. "Construction of All Simple Graphs with at Most 26 Vertices and Transitive Automorphism Group." Ars. Combin. 30, 161-176, 1990.

Royle, G. "Cayley Graphs." http://school.maths.uwa.edu.au/~gordon/remote/cayley/.Royle, G. "Transitive Graphs." http://school.maths.uwa.edu.au/~gordon/trans/.Sloane, N. J. A. Sequence A185959 in "The On-Line Encyclopedia of Integer Sequences."Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 938, 2002.