Spline

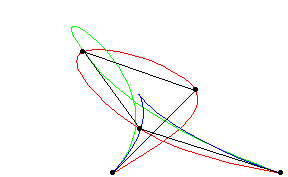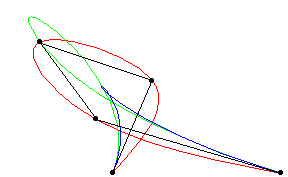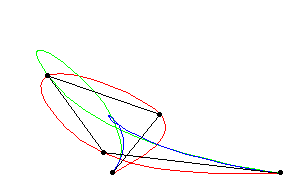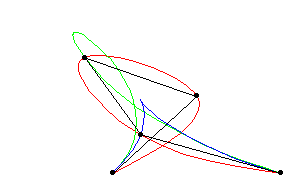
A piecewise polynomial function that can have a locally very simple form, yet at the same time be globally flexible and smooth. Splines are very useful for modeling arbitrary functions, and are used extensively in computer graphics.

Cubic splines are implemented in the Wolfram Language as BSplineCurve[pts, SplineDegree -> 3] (red), Bézier curves as BezierCurve[pts] (blue), and B-splines as BSplineCurve[pts].

REFERENCES:

Bartels, R. H.; Beatty, J. C.; and Barsky, B. A. An Introduction to Splines for Use in Computer Graphics and Geometric Modelling. San Francisco, CA: Morgan Kaufmann, 1998.

de Boor, C. A Practical Guide to Splines. New York: Springer-Verlag, 1978.

Dierckx, P. Curve and Surface Fitting with Splines. Oxford, England: Oxford University Press, 1993.

Micula, G. and Micula, S. Handbook of Splines. Dordrecht, Netherlands: Kluwer, 1999.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Interpolation and Extrapolation." Ch. 3 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 99-122, 1992.

Späth, H. One Dimensional Spline Interpolation Algorithms. Wellesley, MA: A K Peters, 1995.

Weisstein, E. W. "Books about Splines." http://www.ericweisstein.com/encyclopedias/books/Splines.html.