


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-10-2021
Date: 18-12-2021
Date: 24-9-2021
|
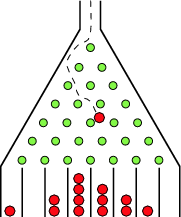
The Galton board, also known as a quincunx or bean machine, is a device for statistical experiments named after English scientist Sir Francis Galton. It consists of an upright board with evenly spaced nails (or pegs) driven into its upper half, where the nails are arranged in staggered order, and a lower half divided into a number of evenly-spaced rectangular slots. The front of the device is covered with a glass cover to allow viewing of both nails and slots. In the middle of the upper edge, there is a funnel into which balls can be poured, where the diameter of the balls must be much smaller than the distance between the nails. The funnel is located precisely above the central nail of the second row so that each ball, if perfectly centered, would fall vertically and directly onto the uppermost point of this nail's surface (Kozlov and Mitrofanova 2002). The figure above shows a variant of the board in which only the nails that can potentially be hit by a ball dropped from the funnel are included, leading to a triangular array instead of a rectangular one.
Each time a ball hits one of the nails, it can bounce right (or left) with some probability 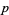 (and
(and 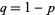 ). For symmetrically placed nails, balls will bounce left or right with equal probability, so
). For symmetrically placed nails, balls will bounce left or right with equal probability, so 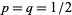 . If the rows are numbered from 0 to
. If the rows are numbered from 0 to 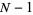 , the path of each falling ball is a Bernoulli trial consisting of
, the path of each falling ball is a Bernoulli trial consisting of 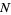 steps. Each ball crosses the bottom row hitting the
steps. Each ball crosses the bottom row hitting the 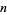 th peg from the left (where
th peg from the left (where 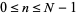 ) iff it has taken exactly
) iff it has taken exactly 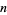 right turns, which occurs with probability
right turns, which occurs with probability
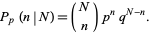 |
This process therefore gives rise to a binomial distribution of in the heights of heaps of balls in the lower slots.
If the number of balls is sufficiently large and 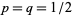 , then according to the weak law of large numbers, the distribution of the heights of the ball heaps will approximate a normal distribution.
, then according to the weak law of large numbers, the distribution of the heights of the ball heaps will approximate a normal distribution.
Some care is needed to obtain these idealized results, however, as the actual distribution of balls depends on physical properties of the setup, including the elasticity of the balls (as characterized by their coefficient of restitution), the radius of the nails, and the offsets of the balls over the funnel's opening when they are dropped (Kozlov and Mitrofanova 2002).
REFERENCES:
Chepelianskii, A. D. and Shepelyansky, D. L. Phys. Rev. Lett. 87, 034101-1, 2001.
Galton, F. Natural Inheritance. New York: Macmillan, 1894.
"Galton's Board or Quincunx." http://www.stattucino.com/berrie/dsl/Galton.html.
Hoover, W. G. In Microscopic Simulations of Complex Hydrodynamic Phenomena (Ed. M. Mareschal and B. L. Holian). New York: Plenum, 1992.
Hoover, W. G. and Moran, B. Phys. Rev. A 40, 5319, 1989.
Kozlov, V. V. and Mitrofanova, M. Yu. "Galton Board." Regular Chaotic Dynamics 8, 431-439, 2002.
Kumič, K. In Unsolved Problems of Noise and Fluctuations: UPoN'99: Second International Conference, Adelaide, Australia 11-15 July 1999 (Ed. D. Abbott and L. B. Kish). Melville: American Institute of Physics, 2000.
Lue, A. and Brenner, H. Phys. Rev. E 47, 3128, 1993.
Moran, B. and Hoover, W. G. J. Stat. Phys. 48, 709, 1987.
Physics at Davidson. "Galton Board." http://webphysics.davidson.edu/Applets/galton4/galton_mean.html.
University of Alabama in Huntsville. "The Galton Board Experiment." http://www.math.uah.edu/stat/applets/GaltonBoardExperiment.xhtml.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
العتبة الحسينية تطلق فعاليات المخيم القرآني الثالث في جامعة البصرة
|
|
|