


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-9-2021
Date: 29-9-2021
Date: 22-12-2021
|
In physics, the word entropy has important physical implications as the amount of "disorder" of a system. In mathematics, a more abstract definition is used. The (Shannon) entropy of a variable 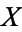 is defined as
is defined as
![H(X)=-sum_(x)P(x)log_2[P(x)]](https://mathworld.wolfram.com/images/equations/Entropy/NumberedEquation1.gif) |
bits, where 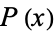 is the probability that
is the probability that 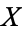 is in the state
is in the state 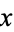 , and
, and 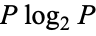 is defined as 0 if
is defined as 0 if 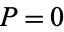 . The joint entropy of variables
. The joint entropy of variables 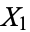 , ...,
, ..., 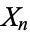 is then defined by
is then defined by
![H(X_1,...,X_n)=-sum_(x_1)...sum_(x_n)P(x_1,...,x_n)log_2[P(x_1,...,x_n)].](https://mathworld.wolfram.com/images/equations/Entropy/NumberedEquation2.gif) |
REFERENCES:
Ellis, R. S. Entropy, Large Deviations, and Statistical Mechanics. New York: Springer-Verlag, 1985.
Havil, J. "A Measure of Uncertainty." §14.1 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 139-145, 2003.
Khinchin, A. I. Mathematical Foundations of Information Theory. New York: Dover, 1957.
Lasota, A. and Mackey, M. C. Chaos, Fractals, and Noise: Stochastic Aspects of Dynamics, 2nd ed. New York: Springer-Verlag, 1994.
Ott, E. "Entropies." §4.5 in Chaos in Dynamical Systems. New York: Cambridge University Press, pp. 138-144, 1993.
Rothstein, J. "Information, Measurement, and Quantum Mechanics." Science 114, 171-175, 1951.
Schnakenberg, J. "Network Theory of Microscopic and Macroscopic Behavior of Master Equation Systems." Rev. Mod. Phys. 48, 571-585, 1976.
Shannon, C. E. "A Mathematical Theory of Communication." The Bell System Technical J. 27, 379-423 and 623-656, July and Oct. 1948. http://cm.bell-labs.com/cm/ms/what/shannonday/shannon1948.pdf.
Shannon, C. E. and Weaver, W. Mathematical Theory of Communication. Urbana, IL: University of Illinois Press, 1963.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|