


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-12-2021
Date: 21-11-2021
Date: 23-11-2021
|
The Schur decomposition of a complex square matrix 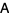 is a matrix decomposition of the form
is a matrix decomposition of the form
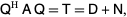 |
(1) |
where 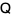 is a unitary matrix,
is a unitary matrix, 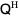 is its conjugate transpose, and
is its conjugate transpose, and 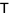 is an upper triangular matrix which is the sum of a
is an upper triangular matrix which is the sum of a 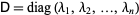 (i.e., a diagonal matrix consisting of eigenvalues
(i.e., a diagonal matrix consisting of eigenvalues 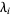 of
of 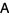 ) and a strictly upper triangular matrix
) and a strictly upper triangular matrix 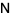 .
.
Schur decomposition is implemented in the Wolfram Language for numeric matrices as SchurDecomposition[m]. The first step in a Schur decomposition is a Hessenberg decomposition. Schur decomposition on an 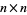 matrix requires
matrix requires 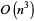 arithmetic operations.
arithmetic operations.
For example, the Schur decomposition of the matrix
![A=[3 2 1; 4 2 1; 4 4 0]](https://mathworld.wolfram.com/images/equations/SchurDecomposition/NumberedEquation2.gif) |
(2) |
is
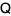 |
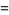 |
![[0.49857 0.76469 0.40825; 0.57405 0.061628 -0.81650; 0.64953 -0.64144 0.40825]](https://mathworld.wolfram.com/images/equations/SchurDecomposition/Inline13.gif) |
(3) |
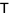 |
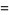 |
![[6.6056 4.4907 -0.82632; 0.00000 -0.60555 1.0726; 0.00000 0.00000 -1.00000],](https://mathworld.wolfram.com/images/equations/SchurDecomposition/Inline16.gif) |
(4) |
and the eigenvalues of 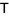 are
are 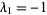 ,
, 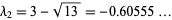 ,
, 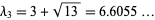 .
.
REFERENCES:
Golub, G. H. and Van Loan, C. F. Matrix Computations, 3rd ed. Baltimore, MD: Johns Hopkins University Press, pp. 312-314, 1996.
Schur, I. "On the Characteristic Roots of a Linear Substitution with an Application to the Theory of Integral Equations." Math. Ann. 66, 488-510, 1909.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|