


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-11-2021
Date: 10-11-2021
Date: 25-9-2021
|
Condorcet's jury theorem states that given a group of voters (a "jury") independently choosing by majority vote between a correct outcome with probability 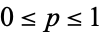 and an incorrect one with probability
and an incorrect one with probability 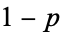 :
:
1. If 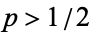 (so that each voter is more likely to vote correctly that incorrectly), adding more voters increases the probability that the majority chooses correctly and the probability of a correct decision approaches 1 as the number of voters increases;
(so that each voter is more likely to vote correctly that incorrectly), adding more voters increases the probability that the majority chooses correctly and the probability of a correct decision approaches 1 as the number of voters increases;
2. If 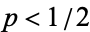 (so that each voter is less likely to vote incorrectly than correctly), adding more voters decreases the probability that the majority chooses correctly and the probability of a correct decision is maximized for a jury of size one.
(so that each voter is less likely to vote incorrectly than correctly), adding more voters decreases the probability that the majority chooses correctly and the probability of a correct decision is maximized for a jury of size one.
REFERENCES:
Condorcet, J.-A.-N. de Caritat, marquis de. "Essai sur l'application de l'analyse à la probabilité des décisions rendues à la pluralité des voix." Paris: Imprimerie Royale, 1785.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
بالصور: ممثل المرجعية العليا الشيخ عبد المهدي الكربلائي يؤم جموع المؤمنين في صلاة عيد الفطر المبارك داخل الصحن الحسيني الشريف
|
|
|