Watt's Curve

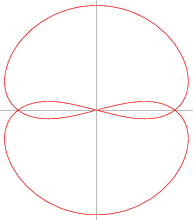
A curve named after James Watt (1736-1819), the Scottish engineer who developed the steam engine (MacTutor Archive). The curve is produced by a linkage of rods connecting two wheels of equal diameter. Let the two wheels have radius 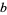 and let their centers be located a distance  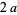apart. Further suppose that a rod of length  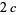is fixed at each end to the circumference of the two wheels. Let  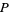be the midpoint of the rod. Then Watt's curve  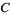is the locus of .

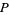The polar equation of Watt's curve is

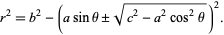(1)

The areas of one of the inner lenses, heart-shaped half-region, and entire enclosed region (which resembles a lemniscate are

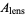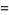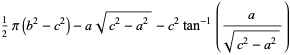			(2)
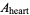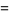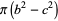			(3)
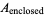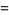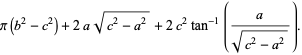			(4)

If 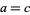, then  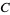is a circle of radius  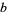with a figure of eight inside it.

REFERENCES:

Lockwood, E. H. A Book of Curves. Cambridge, England: Cambridge University Press, p. 162, 1967.

MacTutor History of Mathematics Archive. "Watt's Curve." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Watts.html.