Remez Algorithm

The Remez algorithm (Remez 1934), also called the Remez exchange algorithm, is an application of the Chebyshev alternation theorem that constructs the polynomial of best approximation to certain functions under a number of conditions. The Remez algorithm in effect goes a step beyond the minimax approximation algorithm to give a slightly finer solution to an approximation problem.

Parks and McClellan (1972) observed that a filter of a given length with minimal ripple would have a response with the same relationship to the ideal filter that a polynomial of degree 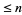 of best approximation has to a certain function, and so the Remez algorithm could be used to generate the coefficients.

In this application, the algorithm is an iterative procedure consisting of two steps. One step is the determination of candidate filter coefficients 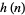 from candidate "alternation frequencies," which involves solving a set of linear equations. The other step is the determination of candidate alternation frequencies from the candidate filter coefficients (Lim and Oppenheim 1988). Experience has shown that the algorithm converges quickly, and is widely used in practice to design filters with optimal response for a given number of taps. However, care should be used in saying "optimal" coefficients, as this is implementation dependent and also depends on fixed or floating-point implementation as well as numerical accuracy.

A FORTRAN implementation is given by Rabiner (1975). A description emphasizing the mathematical foundations rather than digital signal processing applications is given by Cheney (1999), who also spells Remez as Remes (Cheney 1999, p. 96).

REFERENCES:

Cheney, E. W. Introduction to Approximation Theory, 2nd ed. Providence, RI: Amer. Math. Soc., 1999.

DeVore, R. A. and Lorentz, G. G. Constructive Approximation. Berlin: Springer-Verlag, 1993.

Lim, J. S. and Oppenheim, A. V. (Eds). Advanced Topics in Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1988.

Parks, T. W. and McClellan, J. J. "Chebyshev Approximation for Nonrecursive Digital Filters with Linear Phase." IEEE Trans. Circuit Th. 19, 189-194, 1972.

Rabiner, L. W. and Gold, B. Theory and Application of Digital Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1975.

Remez, E. Ya. "Sur le calcul effectif des polynômes d'approximation de Tschebyscheff." C. P. Paris, 337-340, 1934.

Remez, E. Ya. General Computational Methods of Chebyshev Approximation: The Problems with Linear Real Parameters. Atomic Energy Translation 4491. Kiev, 1957.