Little's Law

Little's law states that, under steady state conditions, the average number of items in a queuing system equals the average rate at which the items arrive multiplied by the average time that an item spends in the system. Algebraically, this can expressed as

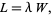where 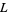 denotes the average number of items in the queuing system,  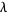is the average number of items arriving per unit time, and  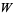is the average waiting time for an item within the system.

Due to its use of general language and its natural conditions with practically no extraneous assumptions, Little's law can be used to asymptotically describe conditions across a vast array of scenarios. For example, Little's law suggests that the average number of students attending a two-year college 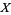 which averages 6,000 first-year student admissions per year is simply .

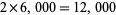REFERENCES:

Little, J. D. C. and Graves, S. C. "Little's Law." In Building Intuition: Insights From Basic Operations Management Models and Principles (Ed. D. Chhajed, and T. J. Lowe). New York: Springer Science+Business Media LLC, pp. 81-100, 2008.

Sigman, K. "Notes on Little's Law." 2009. http://www.columbia.edu/~ks20/stochastic-I/stochastic-I-LL.pdf.