


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-1-2021
Date: 16-8-2020
Date: 17-11-2019
|
A sequence produced by the instructions "reverse, add to the original, then sort the digits." For example, after 668, the next iteration is given by
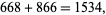 |
so the next term is 1345.
Applied to 1, the sequence gives 1, 2, 4, 8, 16, 77, 145, 668, 1345, 6677, 13444, 55778, 133345, 666677, 1333444, 5567777, 12333445, 66666677, 133333444, 556667777, 1233334444, 5566667777, 12333334444, 55666667777, 123333334444, 556666667777, 1233333334444, ... (OEIS A004000).
Conway conjectured that an initial number leads to a divergent period-two pattern (such as the above in which the numbers of threes and sixes in the middles of alternate terms steadily increase) or to a cycle (Guy 2004, p. 404).
The lengths of the cycles obtained by starting with 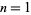 , 2, ... are 0, 0, 8, 0, 0, 8, 0, 0, 2, 0, ... (OEIS A114611), where a 0 indicates that the sequence diverges.
, 2, ... are 0, 0, 8, 0, 0, 8, 0, 0, 2, 0, ... (OEIS A114611), where a 0 indicates that the sequence diverges.
The following table summarizes the first few values of 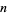 leading to a period of length
leading to a period of length 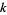 . There are no other periods of length 50 or less for
. There are no other periods of length 50 or less for 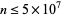 (E. W. Weisstein, Dec. 19, 2005).
(E. W. Weisstein, Dec. 19, 2005).
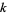 |
OEIS | 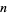 with period with period 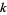 |
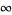 |
A001651 | 1, 2, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 20, ... |
| 2 | A114612 | 9, 18, 27, 36, 45, 54, 63, 69, 72, 78, 81, 87, 90, 96, ... |
| 3 | A114613 | 20169, 20709, 21159, 22149, 23139, 24129, 25119, 26109, ... |
| 8 | A114614 | 3, 6, 12, 15, 21, 24, 30, 33, 39, 42, 48, 51, 57, 60, 66, ... |
| 14 | A114615 | 6999, 7089, 7179, 7269, 7359, 7449, 7539, 7629, ... |
| 18 | A114616 | 29, 38, 47, 49, 56, 58, 65, 67, 74, 76, 83, 85, 92, 94, ... |
REFERENCES:
Cooper, C. and Kennedy, R. E. "Base 10 RATS Cycles and Arbitrarily Long Base 10 RATS Cycles." In Applications of Fibonacci Numbers, Vol. 8. Dordrecht, Netherlands: Kluwer, pp. 83-93, 1999.
Guy, R. K. "Conway's RATS and Other Reversals." Amer. Math. Monthly 96, 425-428, 1989.
Guy, R. K. "Conway's RATS and Palindromes." §F32 in Unsolved Problems in Number Theory, 3rd ed. New York: Springer-Verlag, p. 404, 2004.
Prosper, V. and Veigneau, S. "On the Palindromal Reversal Process." Calcolo 38, 129-140, 2001.
Shattuck, S. and Copper, C. "Divergent RATS Sequences." Fib. Quart. 39, 101-106, 2001.
Sloane, N. J. A. Sequences A001651/M0957, A004000/M1137, A114611, A114612, A114613, A114614, A114615, and A114616 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|