Quotient Space

The quotient space 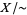 of a topological space  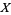and an equivalence relati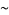on  on 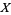 is the set of equivalence classes of points in  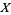(under the equivalence relation 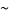) together with the following topology given to subsets of 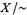: a subset  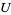of 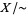 is called open iff  is open in 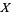. Quotient spaces are also called factor spaces.

This can be stated in terms of maps as follows: if 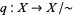 denotes the map that sends each point to its equivalence class in 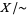, the topology on  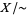can be specified by prescribing that a subset of  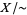is open iff  is open.

In general, quotient spaces are not well behaved, and little is known about them. However, it is known that any compact metrizable space is a quotient of the Cantor set, any compact connected 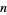-dimensional manifold for  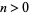is a quotient of any other, and a function out of a quotient space  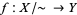is continuous iff the function  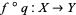is continuous.

Let 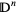 be the closed 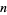-dimensional disk and  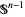its boundary, the 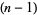-dimensional sphere. Then  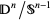(which is homeomorphic to 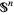), provides an example of a quotient space. Here,  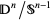is interpreted as the space obtained when the boundary of the 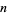-disk is collapsed to a point, and is formally the "quotient space by the equivalence relation generated by the relations that all points in  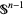are equivalent."

REFERENCES:

Munkres, J. R. Topology: A First Course, 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 2000.