


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-8-2021
Date: 8-5-2021
Date: 22-7-2021
|
The term domain has (at least) three different meanings in mathematics.
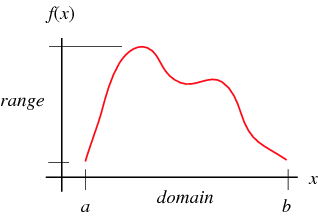
The term domain is most commonly used to describe the set of values 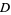 for which a function (map, transformation, etc.) is defined. For example, a function
for which a function (map, transformation, etc.) is defined. For example, a function 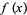 that is defined for real values
that is defined for real values 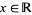 has domain
has domain 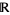 , and is sometimes said to be "a function over the reals." The set of values to which
, and is sometimes said to be "a function over the reals." The set of values to which 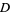 is sent by the function is then called the range.
is sent by the function is then called the range.
Unfortunately, the term range is sometimes used in probability theory to mean domain (Feller 1968, p. 200; Evans et al. 2000). To confuse matters even more, the term "range" is more commonly used in statistics to refer to a completely different quantity, known in this work as the statistical range. As if this wasn't confusing enough, Evans et al. (2000, p. 6) define a probability domain to be the range of the distribution function of a probability density function.
The domain (in its usual established mathematical sense) of a probability density function (and therefore also its distribution function) is available with the undocumented Wolfram Language command DistributionDomain[dist].
The meaning of "domain" in topology is a connected open set.
Another meaning of "domain" is what is more properly known as an integral domain, i.e., a ring that
is commutative under multiplication, has an identity element, and no divisors of 0.
REFERENCES:
Evans, M.; Hastings, N.; and Peacock, B. Statistical Distributions, 3rd ed. New York: Wiley, 2000.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, 1968.
Krantz, S. G. Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 76, 1999.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|