


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-6-2021
Date: 10-8-2021
Date: 9-6-2021
|
An invertible knot is a knot that can be deformed via an ambient isotopy into itself but with the orientation reversed. A knot that is not invertible is said to be noninvertible.
Knots on ten and fewer crossing can be tested in the Wolfram Language to see if they are invertible using the command KnotData[knot, "Invertible"].
Fox (1962, Problem 10, p. 169) pointed out several knots belonging to the standard table that seemed to be noninvertible. However, no noninvertible knots were proven to exist until Trotter (1964) discovered an infinite family, the smallest of which had 15 crossings.

Three prime knots on 9 or fewer crossings are noninvertible: 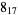 ,
, 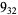 , and
, and 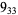 (Cromwell 2004, pp. 297-299). Some noninvertible knots can be obtained in the Wolfram Language as KnotData["Noninvertible"]. The simplest noninvertible knot is (illustrated above) was first postulated to be noninvertible by Fox (1962; Whitten 1972).
(Cromwell 2004, pp. 297-299). Some noninvertible knots can be obtained in the Wolfram Language as KnotData["Noninvertible"]. The simplest noninvertible knot is (illustrated above) was first postulated to be noninvertible by Fox (1962; Whitten 1972).
The following table gives the numbers of noninvertible and invertible knots of 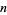 crossings.
crossings.
| type | OEIS | counts |
| noninvertible | A052403 | 0, 0, 0, 0, 0, 0, 0, 1, 2, 33, 187, 1144, 6919, 38118, 226581, 1309875, ... |
| invertible | A052402 | 0, 0, 1, 1, 2, 3, 7, 20, 47, 132, 365, 1032, 3069, 8854, 26712, 78830, ... |
No general technique is known for determining if a knot is invertible. Burde and Zieschang (1985) give a tabulation from which it is possible to extract the noninvertible knots up to 10 crossings.
REFERENCES:
Burde, G. and Zieschang, H. Knots, 2nd rev.ed. Berlin: de Gruyter, 2002.
Cromwell, P. Knots and Links. Cambridge, England: Cambridge University Press, 2004.
Fox, R. H. "A Quick Trip Through Knot Theory." In Topology of 3-Manifolds and Related Topics. Proc. The Univ. of Georgia Institute, 1961. Englewood Cliffs, NJ: Prentice-Hall, pp. 120-167, 1962.
Hoste, J.; Thistlethwaite, M.; and Weeks, J. "The First 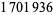 Knots." Math. Intell. 20, 33-48, Fall 1998.
Knots." Math. Intell. 20, 33-48, Fall 1998.
Sloane, N. J. A. Sequences A052402 and A052403 in "The On-Line Encyclopedia of Integer Sequences."
Trotter, H. F. "Noninvertible Knots Exist." Topology 2, 275-280, 1964.
Whitten, W. "Surgically Transforming Links into Noninvertible Knots." Amer. J. Math. 94, 1269-1281, 1972.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|