


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-7-2021
Date: 21-5-2021
Date: 15-8-2021
|

The unknot, also called the trivial knot (Rolfsen 1976, p. 51), is a closed loop that is not knotted. In the 1930s Reidemeister first proved that knots exist which are distinct from the unknot by inventing and making use of the so-called Reidemeister moves and coloring each part of a knot diagram with one of three colors.
The unknot is implemented in the Wolfram Language as KnotData["Unknot"].
The knot sum of two unknots is another unknot.
The Jones polynomial of the unknot is defined to give the normalization
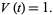 |
(1) |
The unknot has Alexander polynomial 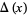 and Conway polynomial
and Conway polynomial 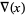
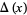 |
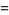 |
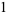 |
(2) |
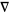 |
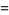 |
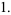 |
(3) |
Surprisingly, there are known examples of nontrivial knots with Alexander polynomial 1, although no such examples occur among the knots of 10 or fewer crossings. An example is the 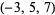 -pretzel knot (Adams 1994, p. 167). Rolfsen (1976, p. 167) gives four other such examples.
-pretzel knot (Adams 1994, p. 167). Rolfsen (1976, p. 167) gives four other such examples.
Haken (1961) devised an algorithm to tell if a knot projection is the unknot. The algorithm is so complicated, however, that it has never been implemented.
REFERENCES:
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 165-169, 1994.
Bar-Natan, D. "The Knot  ." https://www.math.toronto.edu/~drorbn/KAtlas/Knots/0.1.html.
." https://www.math.toronto.edu/~drorbn/KAtlas/Knots/0.1.html.
Haken, W. "Theorie der Normalflachen." Acta Math. 105, 245-375, 1961.
Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., p. 15, 1993.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, 1976.
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 264-265, 1999.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|