


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-7-2021
Date: 14-7-2021
Date: 21-6-2021
|
The study of manifolds having a complete Riemannian metric. Riemannian geometry is a general space based on the line element
 |
with 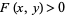 for
for 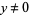 a function on the tangent bundle
a function on the tangent bundle 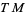 . In addition,
. In addition, 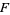 is homogeneous of degree 1 in
is homogeneous of degree 1 in 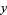 and of the form
and of the form
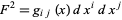 |
(Chern 1996). If this restriction is dropped, the resulting geometry is called Finsler geometry.
REFERENCES:
Besson, G.; Lohkamp, J.; Pansu, P.; and Petersen, P. Riemannian Geometry. Providence, RI: Amer. Math. Soc., 1996.
Buser, P. Geometry and Spectra of Compact Riemann Surfaces. Boston, MA: Birkhäuser, 1992.
Chavel, I. Eigenvalues in Riemannian Geometry. New York: Academic Press, 1984.
Chavel, I. Riemannian Geometry: A Modern Introduction. New York: Cambridge University Press, 1994.
Chern, S.-S. "Finsler Geometry is Just Riemannian Geometry without the Quadratic Restriction." Not. Amer. Math. Soc. 43, 959-963, 1996.
do Carmo, M. P. Riemannian Geometry. Boston, MA: Birkhäuser, 1992.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة لجامعة سومر للمشاركة في حفل التخرج المركزي الخامس
|
|
|