


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-6-2021
Date: 22-7-2021
Date: 10-7-2021
|
An 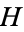 -space, named after Heinz Hopf, and sometimes also called a Hopf space, is a topological space together with a continuous binary operation
-space, named after Heinz Hopf, and sometimes also called a Hopf space, is a topological space together with a continuous binary operation 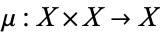 , such that there exists a point
, such that there exists a point 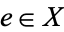 with the property that the two maps
with the property that the two maps 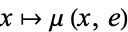 and
and 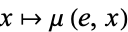 are both homotopic to the identity map
are both homotopic to the identity map 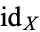 on
on 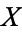 , through homotopies preserving the point
, through homotopies preserving the point 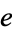 . The element
. The element 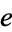 is called a homotopy identity.
is called a homotopy identity.
One should note that authors do not always agree on the definition of an 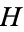 -space. In some texts, the maps given by
-space. In some texts, the maps given by 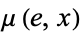 and
and 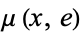 are required to be equal to the identity on
are required to be equal to the identity on 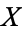 . In others, the two maps are required to be homotopic to the identity as above, but the homotopies need not fix the element
. In others, the two maps are required to be homotopic to the identity as above, but the homotopies need not fix the element 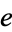 . Fortunately, we have the comforting fact that for any CW-complex, the three definitions above are equivalent.
. Fortunately, we have the comforting fact that for any CW-complex, the three definitions above are equivalent.
For any 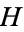 -space
-space 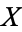 with homotopy identity
with homotopy identity 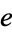 , the fundamental group with base-point
, the fundamental group with base-point 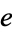 is an Abelian group. Taking another base-point
is an Abelian group. Taking another base-point 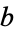 in a path-component of
in a path-component of 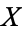 not containing
not containing 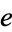 may, however, result in a non-Abelian fundamental group.
may, however, result in a non-Abelian fundamental group.
A deep theorem in homotopy theory known as the Hopf invariant one theorem (sometimes also known as Adams' theorem) states that the only 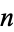 -spheres that are
-spheres that are 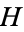 -spaces are
-spaces are 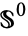 ,
, 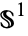 ,
, 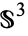 , and
, and 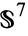 .
.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|