


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-5-2021
Date: 11-5-2021
Date: 6-5-2021
|
In its original form, the Poincaré conjecture states that every simply connected closed three-manifold is homeomorphic to the three-sphere (in a topologist's sense) 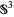 , where a three-sphere is simply a generalization of the usual sphere to one dimension higher. More colloquially, the conjecture says that the three-sphere is the only type of bounded three-dimensional space possible that contains no holes. This conjecture was first proposed in 1904 by H. Poincaré (Poincaré 1953, pp. 486 and 498), and subsequently generalized to the conjecture that every compact
, where a three-sphere is simply a generalization of the usual sphere to one dimension higher. More colloquially, the conjecture says that the three-sphere is the only type of bounded three-dimensional space possible that contains no holes. This conjecture was first proposed in 1904 by H. Poincaré (Poincaré 1953, pp. 486 and 498), and subsequently generalized to the conjecture that every compact 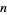 -manifold is homotopy-equivalent to the
-manifold is homotopy-equivalent to the 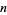 -sphere iff it is homeomorphic to the
-sphere iff it is homeomorphic to the 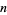 -sphere. The generalized statement reduces to the original conjecture for
-sphere. The generalized statement reduces to the original conjecture for 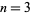 .
.
The Poincaré conjecture has proved a thorny problem ever since it was first proposed, and its study has led not only to many false proofs, but also to a deepening in the understanding of the topology of manifolds (Milnor). One of the first incorrect proofs was due to Poincaré himself (1953, p. 370), stated four years prior to formulation of his conjecture, and to which Poincaré subsequently found a counterexample. In 1934, Whitehead (1962, pp. 21-50) proposed another incorrect proof, then discovered a counterexample (the Whitehead link) to his own theorem.
The 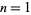 case of the generalized conjecture is trivial, the
case of the generalized conjecture is trivial, the 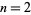 case is classical (and was known to 19th century mathematicians),
case is classical (and was known to 19th century mathematicians), 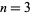 (the original conjecture) appears to have been proved by recent work by G. Perelman (although the proof has not yet been fully verified),
(the original conjecture) appears to have been proved by recent work by G. Perelman (although the proof has not yet been fully verified), 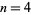 was proved by Freedman (1982) (for which he was awarded the 1986 Fields medal),
was proved by Freedman (1982) (for which he was awarded the 1986 Fields medal), 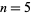 was demonstrated by Zeeman (1961),
was demonstrated by Zeeman (1961), 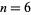 was established by Stallings (1962), and
was established by Stallings (1962), and 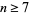 was shown by Smale in 1961 (although Smale subsequently extended his proof to include all
was shown by Smale in 1961 (although Smale subsequently extended his proof to include all 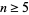 ).
).
The Clay Mathematics Institute included the conjecture on its list of $1 million prize problems. In April 2002, M. J. Dunwoody produced a five-page paper that purports to prove the conjecture. However, Dunwoody's manuscript was quickly found to be fundamentally flawed (Weisstein 2002).
The work of Perelman (2002, 2003; Robinson 2003) established a more general result known as the Thurston's geometrization conjecture from which the Poincaré conjecture immediately follows. Perelman's work has subsequently been verified, thus establishing the conjecture.
REFERENCES:
Adams, C. C. "The Poincaré Conjecture, Dehn Surgery, and the Gordon-Luecke Theorem." §9.3 in The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 257-263, 1994.
Batterson, S. Stephen Smale: The Mathematician Who Broke the Dimension Barrier. Providence, RI: Amer. Math. Soc., 2000. Bing, R. H. "Some Aspects of the Topology of 3-Manifolds Related to the Poincaré Conjecture." In Lectures on Modern Mathematics, Vol. II (Ed. T. L. Saaty). New York: Wiley, pp. 93-128, 1964.
Birman, J. "Poincaré's Conjecture and the Homeotopy Group of a Closed, Orientable 2-Manifold." J. Austral. Math. Soc. 17, 214-221, 1974.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 38-39, 2003.
Brodie, J. "Perelman Explains Proof to Famous Math Mystery." The Daily Princetonian. April 17, 2003.
Clay Mathematics Institute. "The Poincaré Conjecture." http://www.claymath.org/millennium/Poincare_Conjecture/.
Collins, G. P. "The Shapes of Space." Sci. Amer. 291, 94-103, July 2004.
Dunwoody, M. J. "A Proof of the Poincaré Conjecture." http://www.maths.soton.ac.uk/pure/viewabstract.phtml?entry=655. Rev. Apr. 9, 2002.
Freedman, M. H. "The Topology of Four-Differentiable Manifolds." J. Diff. Geom. 17, 357-453, 1982.
Gabai, D. "Valentin Poenaru's Program for the Poincaré Conjecture." In Geometry, Topology, & Physics, Conf. Proc. Lecture Notes Geom. Topol., VI (Ed. S.-T. Yau). Cambridge, MA: International Press, pp. 139-166, 1995.
Gillman, D. and Rolfsen, D. "The Zeeman Conjecture for Standard Spines is Equivalent to the Poincaré Conjecture." Topology 22, 315-323, 1983.
Jakobsche, W. "The Bing-Borsuk Conjecture is Stronger than the Poincaré Conjecture." Fund. Math. 106, 127-134, 1980.
Johnson, G. "A Mathematician's World of Doughnuts and Spheres." The New York Times, April 20, 2003, p. 5.
Milnor, J. "The Poincaré Conjecture." http://www.claymath.org/millennium/Poincare_Conjecture/Official_Problem_Description.pdf.
Milnor, J. W. "The Poincaré Conjecture 99 Years Later: A Progress Report." http://www.math.sunysb.edu/~jack/PREPRINTS/poiproof.pdf.
Nikitin, S. "Proof of the Poincare Conjecture" 22 Oct 2002. http://arxiv.org/abs/math.GT/0210334.
Papakyriakopoulos, C. "A Reduction of the Poincaré Conjecture to Group Theoretic Conjectures." Ann. Math. 77, 250-205, 1963.
Perelman, G. "The Entropy Formula for the Ricci Flow and Its Geometric Application" 11 Nov 2002. http://arxiv.org/abs/math.DG/0211159.
Perelman, G. "Ricci Flow with Surgery on Three-Manifolds" 10 Mar 2003. http://arxiv.org/abs/math.DG/0303109.
Poincaré, H. "Cinquième complément à l'analysis situs." Rend. Circ. Mat. Palermo 18, 45-110, 1904. Reprinted in Oeuvres, Tome VI. Paris, 1953, p. 498.
Œuvres de Henri Poincaré, tome VI. Paris: Gauthier-Villars, pp. 486 and 498, 1953.
Robinson, S. "Russian Reports He Has Solved a Celebrated Math Problem." The New York Times, p. D3, April 15, 2003.
Rourke, C. "Algorithms to Disprove the Poincaré Conjecture." Turkish J. Math. 21, 99-110, 1997.
Rubinstein, J. H. "Polyhedral Minimal Surfaces, Heegaard Splittings and Decision Problems for 3-Dimensional Manifolds." In Geometric Topology. Proceedings of the 1993 Georgia International Topology Conference held at the University of Georgia, Athens, GA, August 2-13, 1993 (Ed. W. H. Kazez). Cambridge, MA: International Press, pp. 1-20, 1997.
Stallings, J. "The Piecewise-Linear Structure of Euclidean Space." Proc. Cambridge Philos. Soc. 58, 481-488, 1962.
Smale, S. "Generalized Poincaré's Conjecture in Dimensions Greater than Four." Ann. Math. 74, 391-406, 1961.
Smale, S. "The Story of the Higher Dimensional Poincaré Conjecture (What Actually Happened on the Beaches of Rio)." Math. Intell. 12, 44-51, 1990.
Smale, S. "Mathematical Problems for the Next Century." Math. Intelligencer 20, No. 2, 7-15, 1998.
Smale, S. "Mathematical Problems for the Next Century." In Mathematics: Frontiers and Perspectives 2000 (Ed. V. Arnold, M. Atiyah, P. Lax, and B. Mazur). Providence, RI: Amer. Math. Soc., 2000.
Thickstun, T. L. "Open Acyclic 3-Manifolds, a Loop Theorem, and the Poincaré Conjecture." Bull. Amer. Math. Soc. 4, 192-194, 1981.
Thompson, A. "Thin Position and the Recognition Problem for 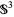 ." Math. Res. Letters 1, 613-630, 1994.
." Math. Res. Letters 1, 613-630, 1994.
Weisstein, E. W. "Poincaré Conjecture Purported Proof Perforated." MathWorld Headline News, Apr. 18, 2002. http://mathworld.wolfram.com/news/2002-04-18/poincare/.
Weisstein, E. W. "Poincaré Conjecture Proved--This Time for Real." MathWorld Headline News, Apr. 15, 2003. http://mathworld.wolfram.com/news/2003-04-15/poincare/.
Whitehead, J. H. C. Mathematical Works, Vol. 2. London: Pergamon Press, 1962.
Zeeman, E. C. "The Generalised Poincaré Conjecture." Bull. Amer. Math. Soc. 67, 270, 1961.
Zeeman, E. C. "The Poincaré Conjecture for 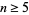 ." In Topology of 3-Manifolds and Related Topics, Proceedings of the University of Georgia Institute, 1961. Englewood Cliffs, NJ: Prentice-Hall, pp. 198-204, 1961.
." In Topology of 3-Manifolds and Related Topics, Proceedings of the University of Georgia Institute, 1961. Englewood Cliffs, NJ: Prentice-Hall, pp. 198-204, 1961.



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|