


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-4-2021
Date: 15-4-2021
Date: 21-3-2021
|
Nonparametric estimation is a statistical method that allows the functional form of a fit to data to be obtained in the absence of any guidance or constraints from theory. As a result, the procedures of nonparametric estimation have no meaningful associated parameters. Two types of nonparametric techniques are artificial neural networks and kernel estimation.
Artificial neural networks model an unknown function by expressing it as a weighted sum of several sigmoids, usually chosen to be logit curves, each of which is a function of all the relevant explanatory variables. This amounts to an extremely flexible functional form for which estimation requires a nonlinear least-squares iterative search algorithm based on gradients.
Kernel estimation specifies 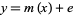 , where
, where 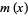 is the conditional expectation of
is the conditional expectation of 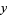 with no parametric form whatsoever, and the density of the error
with no parametric form whatsoever, and the density of the error 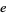 is completely unspecified. The
is completely unspecified. The 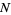 observations
observations 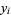 and
and 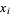 are used to estimate a joint density function for
are used to estimate a joint density function for 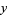 and
and  . The density at a point
. The density at a point 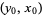 is estimated by seeing what proportion of the
is estimated by seeing what proportion of the 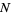 observations are "close to"
observations are "close to" 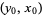 . This procedure involves the use of a function called a kernel to assign weights to nearby observations.
. This procedure involves the use of a function called a kernel to assign weights to nearby observations.
REFERENCES:
Kennedy, P. A Guide to Econometrics, 5th ed. Cambridge, MA: MIT Press, 1998.
Pagan, A. R. and Ullah, A. Non-Parametric Econometrics. Cambridge, England: Cambridge University Press, 1997.
Scott, D. W. Multivariate Density Estimation: Theory, Practice and Visualization. New York: Wiley, 1992.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة لجامعة سومر للمشاركة في حفل التخرج المركزي الخامس
|
|
|