Sample Variance

The sample variance 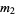 (commonly written  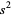or sometimes 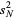) is the second sample central moment and is defined by

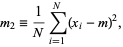(1)

where 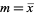 the sample mean and  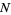is the sample size.

To estimate the population variance 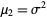 from a sample of  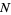elements with a priori unknown mean (i.e., the mean is estimated from the sample itself), we need an unbiased estimat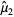or  for 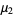. This estimator is given by k-statistic 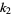, which is defined by

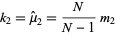(2)

(Kenney and Keeping 1951, p. 189). Similarly, if 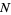 samples are taken from a distribution with underlying central moments 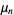, then the expected value of the observed sample variance  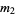is

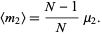(3)

Note that some authors (e.g., Zwillinger 1995, p. 603) prefer the definition

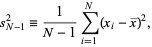(4)

since this makes the sample variance an unbiased estimator for the population variance. The distinction between 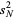 and 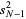 is a common source of confusion, and extreme care should be exercised when consulting the literature to determine which convention is in use, especially since the uninformative notation  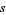is commonly used for both. The unbiased sample variance  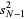is implemented as Variance[list].

Also note that, in general, 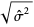 is not an unbiased estimator of the standard deviation  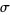even if  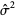is an unbiased estimator for .

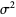REFERENCES:

Evans, M.; Hastings, N.; and Peacock, B. Statistical Distributions, 3rd ed. New York: Wiley, p. 16, 2000.

Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.

Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, 1995.