
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-2-2021
Date: 17-4-2021
Date: 18-4-2021
|
The statistics 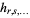 defined such that
defined such that
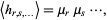 |
where 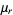 is a central moment. These statistics generalize h-statistics and were originally called "generalized
is a central moment. These statistics generalize h-statistics and were originally called "generalized 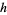 -statistics" (Tracy and Gupta 1974). The term "polyache" was introduced by Rose and Smith (2002, p. 255) by way of analogy with the polykay statistic. Polyaches are commonly defined in terms of power sums, for example
-statistics" (Tracy and Gupta 1974). The term "polyache" was introduced by Rose and Smith (2002, p. 255) by way of analogy with the polykay statistic. Polyaches are commonly defined in terms of power sums, for example
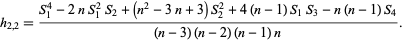 |
Polyaches can be computed using PolyH[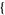 r, s, ...
r, s, ... ] in the Mathematica application package mathStatica.
] in the Mathematica application package mathStatica.
REFERENCES:
Rose, C. and Smith, M. D. Mathematical Statistics with Mathematica. New York: Springer-Verlag, pp. 253-256, 2002.
Tracy, D. S. and Gupta, B. C. "Generalized 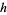 -Statistics and Other Symmetric Functions." Ann. Stat. 2, 837-844, 1974.
-Statistics and Other Symmetric Functions." Ann. Stat. 2, 837-844, 1974.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|