المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Log-Series Distribution |
 1365
 03:03 مساءً
date: 18-4-2021 |
Author : المرجع الالكتروني للمعلوماتيه 
Book or Source : www.almerja.com 
Page and Part : ...|
Read More
Date: 29-3-2021
1449
Date: 20-2-2021
1461
Date: 6-2-2016
1535
|
The log-series distribution, also sometimes called the logarithmic distribution (although this work reserves that term for a distinct distribution), is the distribution of the terms in the series expansion of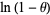 
about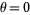 
. It has probability and density functions given by
 |
 |
 |
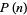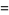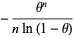(1) |
 |
 |
 |
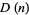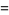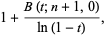(2) |
where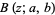 
is the incomplete beta function.
The log-series distribution is implemented as LogSeriesDistribution[theta].
It is properly normalized since
 |
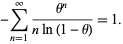(3) |
The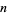 
th raw moment is given by
 |
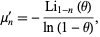(4) |
where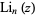 
is a polylogarithm.
The mean, variance, skewness, and kurtosis excess
 |
 |
 |
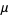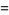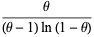(5) |
 |
 |
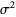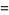![-(theta[theta+ln(1-theta)])/((theta-1)^2[ln(1-theta)]^2)](https://mathworld.wolfram.com/images/equations/Log-SeriesDistribution/Inline17.gif) |
(6) |
 |
 |
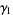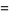![(2theta^2+3thetaln(1-theta)+(1+theta)ln^2(1-theta))/(ln(1-theta)[theta+ln(1-theta)]sqrt(-theta[theta+ln(1-theta)]))ln(1-theta)](https://mathworld.wolfram.com/images/equations/Log-SeriesDistribution/Inline20.gif) |
(7) |
 |
 |
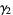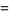![(6theta^3+12theta^2ln(1-theta)+theta(7+4theta)ln^2(1-theta)+(1+4theta+theta^2)ln^3(1-theta))/(theta[theta+ln(1-theta)]^2).](https://mathworld.wolfram.com/images/equations/Log-SeriesDistribution/Inline23.gif) |
|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|
