Elliptic Pseudoprime

Let 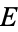 be an elliptic curve defined over the field of rationals  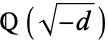having equation

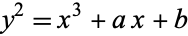with 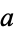 and 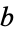 integers. Let  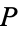be a point on  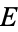with integer coordinates and having infinite order in the additive group of rational points of 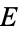, and let  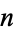be a composite natural number such that 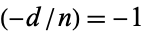, where  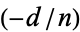is the Jacobi symbol. Then if

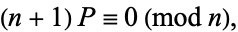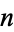 is called an elliptic pseudoprime for .

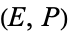REFERENCES:

Balasubramanian, R. and Murty, M. R. "Elliptic Pseudoprimes. II." In Séminaire de Théorie des Nombres, Paris 1988-1989 (Ed. C. Goldstein). Boston, MA: Birkhäuser, pp. 13-25, 1990.

Gordon, D. M. "The Number of Elliptic Pseudoprimes." Math. Comput. 52, 231-245, 1989.

Gordon, D. M. "Pseudoprimes on Elliptic Curves." In Number Theory--Théorie des nombres:Proceedings of the International Number Theory Conference Held at Université Laval in 1987 (Ed. J. M. DeKoninck and C. Levesque). Berlin: de Gruyter, pp. 290-305, 1989.

Miyamoto, I. and Murty, M. R. "Elliptic Pseudoprimes." Math. Comput. 53, 415-430, 1989.

Ribenboim, P. The New Book of Prime Number Records, 3rd ed. New York: Springer-Verlag, pp. 132-134, 1996.